Student-t 분포는 표본평균을 이용해 정규분포의 평균을 측정할 때 사용되는 분포로 표준정규분포를 따르는 확률변수 $Z$와 자유도가 $v$인 카이제곱 분포를 따르는 확률변수 $V$로 다음과 같이 정의하면 확률변수 $T$는 자유도가 $v$인 t-분포를 따릅니다.
$T=\frac{Z}{\sqrt{\frac{V}{v}}}$
정규분포 $N(\mu, \sigma^2)$에서 추출한 $n$개의 표본 $X_1, ..., X_n$에 대해 표본평균 $X_m = \frac{1}{n}(X_1+...+X_n)$, 표본분산 $S^2=\frac{1}{n-1}\sum(X_i-X_m)^2$라 할 때, $V=(n-1)\frac{S^2}{\sigma^2}$는 자유도가 $n-1$인 카이제곱 분포를 따릅니다. (Cochran의 정리)
$Z=(X_m-\mu)\frac{\sqrt{n}}{\sigma}$로 정의하고 위의 $V$의 정의와 함께 $T$를 다시 다음과 같이 정리할 수 있고,
$T=\frac{Z}{\sqrt{\frac{V}{v}}}=(X_m-\mu)\frac{\sqrt{n}}{S}$
모분산인 $\sigma^2$가 사용되지 않으므로 분산을 모를 때의 평균값 $\mu$를 추정하는데 사용이 가능합니다. t-분포는 아래와 같이 정의되며, 자유도 $v$에 따라 모양이 달라지면서 자유도가 커질수록 정규분포 모양에 가까워 집니다.


t-분포는 원점에 대해 좌우대칭이며 보통 표본 수가 30 이상이면 표준정규분포와 가깝다고 할 수 있습니다. 즉, 표본의 크기가 30보다 작으면 t-분포를 사용해야 합니다.
In python
t-분포 또한 scipy.stats의 t 함수를 이용해 쉽게 분포를 파악할 수 있습니다. 먼저 확률분포 $X$를 정의하고,
import numpy as np
X = np.linspace(-5, 5, 101)자유도에 따라 t-분포를 그려보면 다음과 같은 결과를 볼 수 있습니다.
import matplotlib.pyplot as plt
from scipy.stats import t
for i in np.arange(10)+1:
plt.plot(X, t(i).pdf(X))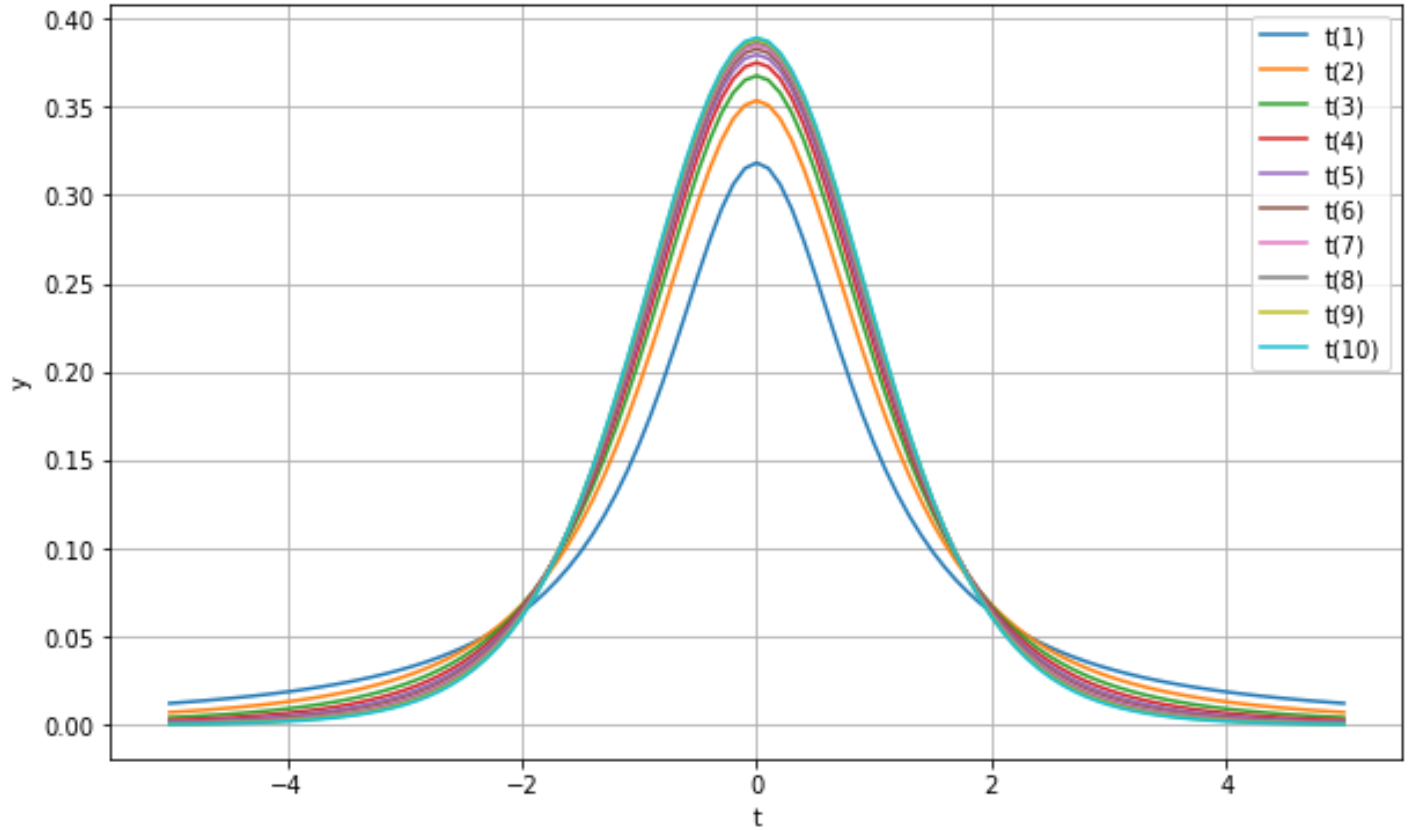
'Theory > Statistics' 카테고리의 다른 글
| 파이썬으로 보는 통계 (6) - F-검정을 이용한 등분산검정 (2) | 2021.04.02 |
|---|---|
| 파이썬으로 보는 통계 (5) - F-분포 (0) | 2021.04.02 |
| 파이썬으로 보는 통계 (4) - 카이제곱 검정 (1) | 2021.04.02 |
| 파이썬으로 보는 통계 (3) - t-검정 (0) | 2021.04.02 |
| 파이썬으로 보는 통계 (1) - 카이제곱 분포 (0) | 2021.04.01 |



