회귀 분석 (Regression) 이란 어떤 변수가 다른 변수에 어떻게 영향을 주는지 설명하는 분석 방법으로 영향을 주는 변수 (독립 변수, independent variable) 와 영향을 받는 변수 (종속 변수, dependent/response variable) 로 구성되어 종속 변수 1개, 독립 변수가 1개일 때는 단순 회귀 분석 (simple regression), 독립 변수가 2개 이상일 때는 다중 회귀 분석 (multiple regression) 이라 불립니다.
이번 포스트에서 살펴볼 내용은 회귀 분석에서 가장 기본적인 단순 선형 회귀 모델 (simple linear regression) 입니다.
Simple linear regression
단순 회귀 분석은 일반적으로 Classical Linear Regression Model 로 다음과 같은 7가지 가정을 전제합니다.
1) 두 변수 간 선형관계가 있어야 합니다.
2) 표분 추출이 무작위하게 이뤄저야 합니다.
3) 데이터가 2개 이상이어야 합니다. 이는 직선을 그리기 위해서는 최소 2개 점이 있어야 합니다.
4) Zero-conditional mean, 주어진 $X$ 값에서 오차의 평균은 0이 됩니다. ($E(\epsilon_i | X_i) = 0$)
5) Homoskedascitiy (등분산성), 모든 $X$에 잉어 오차들이 같은 정도로 펴져 있어야 합니다. ($Var(\epsilon_i)=\sigma^2$)
6) Independence (독립성), 오차항들끼리는 독립이어야 하며 어떤 관계를 가지면 안됩니다. ($Cov(\epsilon_i, \epsilon_j)=0 ,i \neq j$)
7) Normality (정규성), 각 $X_i$에서 오차들끼리 정규분포를 이룹니다.
보면 4부터 7까지는 오차 $\epsilon$에 대한 전제로 fitting을 한 이후의 잔차 (residual, $e$)를 통해 각 가정이 맞는지 검정합니다.

위와 같은 데이터가 있을 때 모든 점을 지나는 직선 (선형 모델)은 존재하지 않으나 어떠한 직선을 기준으로 데이터 점들이 랜덤하게 산개했다고 판단할 수 있습니다. 즉, 정확한 함수 형태의 직선은 존재하지 않으나 독립 변수인 Temperature 와 종속 변수인 Yield 사이에 통계적인 관계가 있다고 추정할 수 있겠죠. 이러한 관계를 다음 수식으로 모델링 합니다.
$Y = \beta_0 + \beta_1 x + \epsilon$
$\beta_0, \beta_1$은 회귀 계수로 $\beta_0$은 절편, $\beta_1$은 기울기이며, $\epsilon$은 오차항으로 독립 변수가 종속 변수에 주는 영향력을 제외한 것입니다. $\epsilon$은 위 가정 4-7에 의해 평균이 0이고 분산이 $\sigma^2$인 정규 분포를 따른다고 가정하기 때문에 관측값 $Y=E[Y]+\epsilon$으로 표현할 수 있으며 다음 그림과 같이 해석할 수 있습니다.

Fitting
주어진 데이터를 가장 잘 설명하는 $\beta_0, \beta_1$은 어떻게 구할 수 있을까요? 종속 변수와 독립 변수의 관계를 잘 나타낸다는 것은 $(x,Y)$의 좌표로 나타낸 점들에 가장 가까이 있는 직선을 찾는 것으로 바꾸어 말하면 모든 점들과의 거리의 합이 최소가 되는 직선을 찾는 것입니다. 다음과 같이 SSE (Sum of Squared Error) 를 정의하고,
$SSE = \sum_i e_i^2 = \sum_i |Y_i - \hat{Y}_i|^2 = \sum_i |Y_i - \beta_0 - \beta_1 x_i|^2$
이를 최소 제곱법 (least squared method) 라는 방법을 통해 최적의 $\beta_0, \beta_1$을 구할 수 있습니다.

$\bar{x}$와 $\bar{y}$는 각각 $x$와 $y$의 평균을 말하고 최종적인 $y$의 추정치는 $\hat{y}=\hat{\beta}_0 + \hat{\beta}_1 x$ 와 같이 표현할 수 있습니다. 이때 추정치 $\hat{y}_i$와 실제값 $y_i$의 차이를 residual 이라 하고 $e_i=y_i-\hat{y}_i$로 표현합니다.
Hypothesis tests
우리는 주어진 데이터를 통계적인 방법으로 분석했습니다. 그렇다면, 위의 방법으로 구한 회귀 계수 $\hat{\beta}_0$, $\hat{\beta}_1$은 통계적으로 얼마나 유의미한지 어떻게 알 수 있을까요?
회귀 계수의 유의성에 대한 통계적 검정은 회귀 계수의 추정값인 $\hat{\beta}_0, \hat{\beta}_1$이 0이냐 그렇지 않느냐를 통계적으로 검정하는 것으로 t-검정을 이용합니다. 특히 종속 변수에 대한 독립 변수의 영향력과 관련된 $\hat{\beta}_1$에 대해서 검정하기 위해서는
귀무 가설 ($H_0$): 독립 변수는 종속 변수에 영향을 주지 않는다 ($\hat{\beta}_1=0$)
대립 가설 ($H_1$): 독립 변수는 종속 변수에 영향을 준다 ($\hat{\beta}_1\neq 0$)
라는 가설을 세우고 t-검정을 통해 양측 검정하고 다음과 같은 순서로 이루어집니다.
1) 먼저 회귀계수의 분산을 구하려면 모회귀선 오차항의 분산을 알아야 되는데, 모수에 대한 정보가 없으므로 오차의 표본인 잔차 (SSE)를 이용하여 잔차의 분산으로 오차항의 분산을 추정합니다.
$s^2=\frac{SSE}{n-2}=\frac{\sum e_i^2}{n-2}$
표본분산에서 모분산을 구할 때 $n-1$을 나눈다는 것을 알고 있을겁니다. 이는 표본분산의 기대값이 모분산의 $\frac{n-1}{n}$에 수렴하므로 편향되지 않는 (unbiased) 모분산 추정을 위해 $\frac{n}{n-1}$을 나눠주기 때문인데요. 잔차분석에 대해서 $n-2$를 나누는 이유도 비슷합니다.
2) 회귀계수 추정값의 분산 (회귀계수의 표준오차)를 구합니다. 위의 7가지 가정이 모두 만족한다면 $\hat{\beta}_1 \sim N(\beta_1, Var(\hat{\beta}_1)$ 을 따르게 되고 $\hat{\beta}_1$의 분산은 오차항의 분산을 $x$ 편차 제곱합으로 나눠준 값으로 다음 수식과 같이 구할 수 있으며 모분산을 보르므로 잔차항의 분산 $s$를 이용해 구하게 됩니다.

3) 표본평균과 표본분산으로 모평균을 추정하기 위해 t-검정을 이용합니다. t 통계량은 (표본평균-모평균)/(표준오차) 로 구할 수 있고 단순회귀분석에서는 자유도가 $n-2$ 인 t-분포를 따르게 됩니다. 따라서 t-분포 상의 t 통계치를 이용해서 얻은 p-value를 통해 계수가 통계적으로 유의한지 확인할 수 있습니다. t 통계량이 크면 p-value가 작아지기 때문에 귀무가설을 기각하고 대립가설인 $X$와 $Y$ 사이에 상관관계가 있다고 결론 내릴 수 있습니다.

Example
보스턴 주택 데이터는 506개의 데이터와 14개의 컬럼으로 이루어진 데이터 셋으로 주택 가격에 영향을 미치는 변수 파악을 위해 자주 사용되는 데이터 입니다. 먼저 시각적으로 상관 계수를 파악하기 위해 seaborn 함수의 heatmap을 이용합니다.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
df = pd.read_csv('housing_data.txt', sep='\s+')
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
'''
LSTAT: 모집단의 하위계층의 비율
INDUS: 비소매업종이 아닌 상업지역 비율
NOX: 일산화질소 농도 (10ppm 당)
RM: 주택의 평균 방 개수
MEDV: 본인 소유의 주택가격 (중앙값)
'''
cm = np.corrcoef(df[cols].values.T)
hm = sns.heatmap(cm,
cbar=True,
annot=True,
square=True,
fmt='.2f',
annot_kws={'size': 15},
yticklabels=cols,
xticklabels=cols)
plt.tight_layout()
plt.show()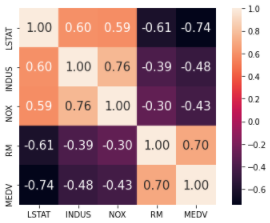
파이썬에서의 선형 회귀 분석은 sklearn.linear_model 모듈의 LinearRegressoin 함수를 이용해 수행할 수 있습니다. 여기서는 RM을 독립 변수로 MEDV를 종속 변수로 하여 단변량 선형 회귀 분석을 수행해 보도록 하겠습니다.
from sklearn.linear_model import LinearRegression
slr = LinearRegression(fit_intercept=True)
X = df[['RM']].values
y = df['MEDV'].values
slr.fit(X, y)
print('기울기: %.3f' % slr.coef_[0])
print('절편: %.3f' % slr.intercept_)
import matplotlib.pyplot as plt
plt.scatter(X, y, c='steelblue', edgecolor='white', s=70)
plt.plot(X, slr.predict(X), color='black', lw=2)
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000s [MEDV]')
plt.show()
RANSAC
위의 선형 회귀 모델 결과를 보았을 때 어느 정도 fitting이 잘 되었다고 할 수 있지만 이상치가 굉장히 많습니다. 선형 회귀 모델은 이상치에 크게 영향을 받는 모델로 데이터의 아주 작은 일부분이 모델 추정에 큰 영향을 미치게 됩니다. 이때 사용할 수 있는 방법으로 RANSAC (RANdom SAmple Consensus) 가 있습니다.
RANSAC은 랜덤하게 샘플을 만들어서 훈련하는 방식으로 랜덤하게 일부 샘플을 선택하여 모델을 훈련하고 훈련된 모델에서 다른 모든 데이터를 테스트해 입력한 허용 오차 안에 속한 데이터를 정상적인 데이터로 추가해서 다시 훈련합니다. 이 과정을 반복하여 성능이 사용자가 지정한 임계값에 도달하거나 지정된 반복 횟수에 도달하면 알고리즘을 종료합니다.
파이썬에서는 sklearn.linear_model 모듈의 RANSACRegressor 라는 함수를 통해 쉽게 구현이 가능합니다. RANSACRegressor 에는 초기에 랜덤하게 선택될 min_samples, 정상 데이터라 판단할 residual_threshold, 반복 횟수 max_trials, 오차 측정 함수를 지정하는 loss 등의 파라미터로 구성되어 있습니다.
from sklearn.linear_model import RANSACRegressor
ransac = RANSACRegressor(LinearRegression(),
max_trials=100,
min_samples=50,
loss='absolute_loss',
residual_threshold=5.0,
random_state=0)
## 선형 회귀분석 수행
ransac.fit(X, y)
## 데이터들이 오차 범위 내에 있는지 여부를 저장한 배열을 가져와서 저장
inlier_mask = ransac.inlier_mask_
## 배열의 값을 반대로 만들어서 저장
outlier_mask = np.logical_not(inlier_mask)
## 그래프를 그릴 범위 설정
line_X = np.arange(3, 10, 1)
## 그릴 범위에 해당하는 데이터의 예측값 가져오기
line_y_ransac = ransac.predict(line_X[:, np.newaxis])
## 실제 데이터를 산점도로 표현
plt.scatter(X[inlier_mask], y[inlier_mask],
c='steelblue', edgecolor='white',
marker='o', label='Inliers')
plt.scatter(X[outlier_mask], y[outlier_mask],
c='limegreen', edgecolor='white',
marker='s', label='Outliers')
## 예측 모델을 선 그래프로 표현
plt.plot(line_X, line_y_ransac, color='black', lw=2)
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000s [MEDV]')
plt.legend(loc='upper left')
print('기울기: %.3f' % ransac.estimator_.coef_[0])
print('절편: %.3f' % ransac.estimator_.intercept_)
plt.show()
'Theory > Statistics' 카테고리의 다른 글
| Regression - 다중 선형 회귀 (0) | 2021.04.15 |
|---|---|
| Regression - R-square (0) | 2021.04.15 |
| 파이썬으로 보는 통계 (7) - 분산분석, ANOVA (0) | 2021.04.02 |
| 파이썬으로 보는 통계 (6) - F-검정을 이용한 등분산검정 (2) | 2021.04.02 |
| 파이썬으로 보는 통계 (5) - F-분포 (0) | 2021.04.02 |



