t-SNE (t-distributed Stochastic Neighbor Embedding) 는 2008년에 Laurens van der Maaten이 발표한 차원 축소 기법으로 고차원 시각화에 많이 쓰이는 방법입니다. 전체 데이터에 대해서 선형 변환을 적용해 분산이 큰 principle component를 뽑아내는 PCA는 고차원 데이터의 복잡한 관계를 저차원으로 매핑하는 능력이 부족합니다. t-SNE는 고차원 manifold 상에 놓여진 데이터 간의 유사도를 저차원에서도 유지할 수 있도록 저차원 embedding 벡터를 학습함으로써 고차원 상의 복잡한 비선형 관계를 저차원 상에서도 잘 표현할 수 있도록 고안되었습니다.
Stochastic neighbor embedding
t-SNE는 SNE (Stochastic Neighbor Embedding)을 개량한 것이므로 먼저 SNE에 대해 살펴보겠습니다. SNE란 고차원에 존재하는 데이터 $x$의 이웃 간의 거리를 저차원 $y$에 대해서도 최대한 보존하도록 하는 알고리즘입니다. Stochasitc 이란 말에서 알 수 있듯이 거리 정보를 유클리디안 거리같은 스칼라 값이 아닌 확률적으로 나타냅니다.
먼저 고차원 공간에서 데이터 $x_i$가 주어졌을 때 이웃 $x_j$ 가 선택될 확률 $p_{j|i}$과 저차원에 임베딩된 $y_i$가 주어졌을 때 $y_j$ 가 선택될 확률 $q_{j|i}$를 정의합니다. $p_{j|i}$에서의 $\sigma_i$는 $x_i$에 따른 Gaussian 분포의 분산으로 각 데이터마다 밀집되거나 흩어져있는 정도가 다르므로 각각 다르게 설정하며 $p_{i|i}=0$으로 둡니다. (Softmax 형태와 비슷합니다)
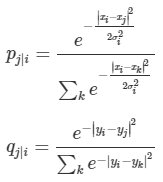
이를 그림으로 표현하면 Figure 1과 같습니다. 빨간색 데이터를 중심으로 근처에 있는 점이 뽑힐 확률은 매우 높지만 먼 거리에 있는 점이 뽑힐 확률은 매우 낮게 되겠죠.

하지만 $p_{i|j}$와 $p_{j|i}$가 대칭적이지는 않습니다. Figure 1/2를 비교해보면 빨간점/초록색점에 대한 분포 위치가 다른 것을 볼 수 있습니다. 이는 당연하게도 각 데이터마다 밀집도가 다르니 $\sigma$가 다르게 설정되어 다른 분포가 되버리기 때문입니다.

$x_i$에 대해서 $\sigma_i$를 각각 다르게 설정하였습니다. 이는 $x_i$ 근처에 많은 데이터가 밀집될 경우 $\sigma_i$가 작은 것이 좋을 것이며 반대의 경우에는 $\sigma_i$가 큰 것이 좋을 것이기 때문입니다. 따라서 $\sigma_i$에 따른 $P_i$의 분포가 제각각 달라지게 되는데 $\sigma_i$가 클수록 분산이 커져 엔트로피가 증가하게 됩니다. SNE에서는 다음과 같이 Perplexity를 정의하여 지정한 perplexity를 만족하는 $\sigma_i$를 이진 탐색으로 찾습니다. (5에서 50 사이로 선택합니다.)
$Perp(P_i) = 2^{H(P_i)}$
$H(P_i) = -\sum_j p_{j|i} log p_{j|i}$
SNE의 목적은 $p,q$ 분포의 차이가 최대한 작게끔 만들어주는 것입니다. 올바른 차원 축소가 이루어졌다면 고차원에서 이웃으로 뽑힐 확률과 저차원에서 이웃으로 뽑힐 확률이 비슷할 것이니까요. 이를 위해 Kullback-Leibler divergence 를 목적함수로 사용합니다.
$C = \sum_i KL(P_i||Q_i) = \sum_i \sum_j p_{j|i}log \frac{p_{j|i}}{q_{j|i}}$
이후 $y_i$에 대해 gradient descent 방법을 적용하여 최적의 $y_i$를 찾습니다.

t-SNE
SNE의 목적 함수 $\sum_i KL(P_i|Q_i)$는 KL-divergence 특성상 대칭적이지 않습니다. 즉, $p$가 높고 $q$가 낮을 때는 비용이 높지만 $p$가 낮고 $q$가 높을 때에는 비용이 높아야하지만 낮습니다. 따라서 t-SNE에서는 SNE에서의 조건부 확률 $p_{j|i}$가 아니라 결합확률분포 $p_{ij}=\frac{p_{j|i}+p_{i|j}}{2}$를 정의하여 목적함수를 재정의합니다.
$C = \sum_i KL(P_i||Q_i) = \sum_i \sum_j p_{ij}log \frac{p_{ij}}{q_{ij}}$
$p_{ij}$를 Equation 1과 같이 설정하지 않는 이유는 $x_i$가 이상치일때 $p_{ij}$가 거의 모든 값에 작을 것이기 때문에 목적함수에 거의 영향을 끼치지 않기 때문입니다. 따라서 $x_i$에서 바라본 $x_j$와 $x_j$에서 바라본 $x_i$를 모두 고려하는 대칭적인 $\frac{p_{j|i}+p_{i|j}}{2n}$ 를 사용합니다. ($\sum_j p_{ij} > \frac{1}{2n}$로 각 데이터의 확률분포가 너무 낮지 않게 만들어주는 효과가 있습니다.) 마찬가지로 $y_i$에 대해 gradient descent 방법을 적용하여 최적의 $y_i$를 찾습니다.

SNE에서 전제하는 확률분포는 Gaussian 분포입니다. 하지만 Gaussian 분포는 꼬리가 두껍지 않아 $i$ 기준에서 적당히 떨어져 있는 $j$와 멀리 떨어진 $k$가 선택될 확률의 차이가 크지 않은데 이를 crowding problem이라 합니다. 따라서 저차원 공간에서 heavy-tailed (확률 분포의 꼬리부분이 두터운 분포) t-distribution을 $q_{ij}$로 사용합니다. 이때의 t-분포는 자유도가 1인 분포로 Cauchy distribution 과 같습니다. (고차원에서는 가우시안 분포를 그대로 사용합니다.)


바꾼 $q_{ij}$를 $C$에 삽입하고 $y_i$에 대해 gradient descent 방법으로 학습하며 전체 알고리즘은 다음과 같습니다.


In python
파이썬에서는 sklearn.manifold 모듈의 TSNE를 사용하여 시각화할 수 있습니다. 중요한 파라미터는 다음과 같습니다.
| Parameters | Description |
| n_components | 임베딩 공간의 차원으로 디폴트 값은 2입니다. |
| perplexity | 디폴트로 30이 지정되어 있고 일반적으로 5-50 사이의 값을 사용합니다. 이 값에 따라 결과가 달라지며 크게 지정할수록 $\sigma$가 커지므로 global structure를 유지하려 하고, 작게 지정할수록 $\sigma$가 작아지므로 local structure를 유지하려 합니다. |
| n_iter | Gradient descent를 수행하는 횟수입니다. |
| metric | 확률 분포를 정의할 때 사용하는 거리 metric으로 디폴트로 'euclidean'이 사용됩니다. |
import numpy as np
from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
digits = load_digits()
x, y = digits.data[:500], digits.target[:500]
X_2d = TSNE(n_components=2).fit_transform(x)
target_ids = range(len(digits.target_names))
from matplotlib import pyplot as plt
plt.figure(figsize=(6, 5))
colors = 'r', 'g', 'b', 'c', 'm', 'y', 'k', 'w', 'orange', 'purple'
for i, c, label in zip(target_ids, colors, digits.target_names):
plt.scatter(X_2d[y == i, 0], X_2d[y == i, 1], c=c, label=label)
plt.legend()
plt.show()
홍머스 정리
- $q_{j|i}$ 계산에서는 $\sigma$를 데이터마다 다르게 두지 않고 $\frac{1}{\sqrt{2}}$로 모두 동일하게 설정한다. 고차원에서 $\sigma$를 다르게 두었음에도 저차원에서는 같게 둠으로써 일정 정보를 잃어버리게 된다. 계산 상의 이득인가?

참조
- lovit.github.io/nlp/representation/2018/09/28/tsne/
- m.blog.naver.com/xorrms78/222112752837
- ratsgo.github.io/machine%20learning/2017/04/28/tSNE/
- scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html
- erdem.pl/2020/04/t-sne-clearly-explained
- Visualizing Data using t-SNE
'Machine Learning Models > Classic' 카테고리의 다른 글
| Dimension Reduction - t-SNE (2) (0) | 2021.05.18 |
|---|---|
| XGBOOST 동작 원리 (0) | 2021.05.15 |
| Dimension Reduction - PCA (0) | 2021.04.20 |
| Classification - Metrics (2) (1) | 2021.04.19 |
| Classification - Metrics (1) (0) | 2021.04.19 |



