2017년 NIPS 에서 발표된 구글의 Transformer 구조는 language modeling, neural machine translator 등의 NLP 계에 혁신을 불어일으킨 논문으로 BERT, GPT 등의 구조의 기반이 되었고 다양한 분야로의 접목이 활발히 연구되고 있는 매우 중요한 neural networks 구조 중 하나입니다. Transformer 가 등장하기 전에는 RNN (LSTM / GRU), Convolution 등으로 sequence 모델링을 수행했었는데요, Transformer 는 recurrence, convolution 의 개념을 아예 배제하고 순수히 attention 으로 구성되어 기존 RNN, CNN 계열에 비해 속도와 성능이 모두 우월한 모델입니다.
Overview
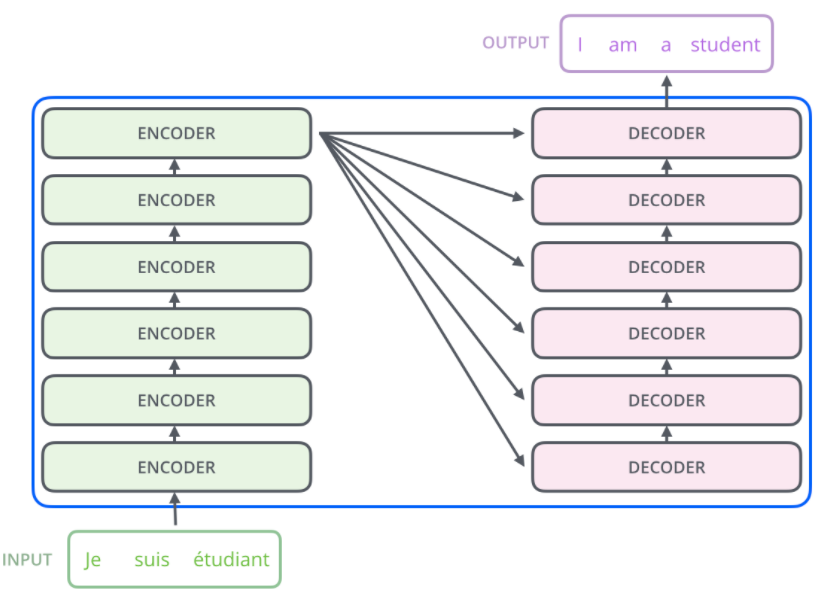
Machine translation 을 수행한다면 Figure 1과 같이 입력 문장이 Transformer 모델에 들어가 번역된 출력 문장이 나오게 될겁니다.

Figure 1에서 black box 로 되어있는 Transformer 구조를 열어보면 Figure 2와 같이 여러 개의 encoder, decoder 로 구성되어 있습니다. Encoder, decoder 개수는 6개이지만 하이퍼파라미터로 조절이 가능합니다.
Encoder
Encoder 는 입력 문장을 받아 이를 각 위치에 따른 representation 으로 표현합니다. 모두 같은 구조를 가지고 있으며 파라미터를 공유하지 않습니다. 개별적인 encoder 는 Figure 3과 같이 1) self-attention, 2) feed-forward 두 개의 sublayer 로 구성되어 있습니다. Self-attention 은 입력으로 들어온 시퀀스에 대해 각 위치의 벡터가 다른 위치의 벡터와 어떠한 관계를 가지는지 모델링합니다. Self-attention 이후에는 각 위치별로 똑같은 feed-forward network 가 적용됩니다.

이 과정을 그림으로 표현하면 Figure 4와 같습니다. 먼저 문장의 단어를 수치화해서 표현하기 위해 입력 단에서 임베딩이 512 차원에 대하여 적용되고 각 위치별로 1) self-attention, 2) feed-forward 가 적용됩니다. 각 sublayer 의 출력 차원은 추후 residual connection 까지 고려하여 임베딩 차원과 같이 $d_{model}=512$ 로 적용합니다.

Decoder
Decoder 또한 encoder 와 매우 유사하며 encoder 의 sublayer 를 모두 가지고 있습니다. 단, encoder 로부터 나온 attention 결과를반영하기 위한 encoder-decoder attention sublayer 가 추가됩니다. Figure 5와 같이 decoder 는 1) self-attention, 2) encoder-decoder attention, 3) feed-forward 세 개의 sublayer 로 구성됩니다.

Self-attention
Self-attention 이란 무엇일까요? "self" 라는 말에서 알 수 있듯이 자기 자신에 대해 주목한다는 뜻일겁니다. 즉, 하나의 문장에 대해서 각 위치의 단어 별로 어느 위치의 단어와 연관이 있는지 파악하겠다는 것이죠. 예를 들어, "The animal didn't cross the street because it was too tired." 라는 문장이 있을 때 "it" 이 "animal" 을 나타낸다는 것은 사람은 쉽게 알 수 있지만 컴퓨터는 그러질 못합니다. 따라서 self-attention 을 이용하여 "it" 이 "animal" 과 매우 연관이 있다는 것을 알려주고자 하는 것이죠. 즉, 입력의 특정 위치에 대해서 다른 위치의 값들과의 연관성을 파악하여 해당 위치에 대한 representation 을 잘 추출하고자 하는 것이 self-attention 의 목적입니다.
그렇다면 self-attention 이 어떠한 과정을 통해 연산되는지 파악해 보겠습니다. 먼저 attention 을 위해 query/key/value 3가지 벡터가 필요하며 입력 $x$로부터 query/key/value 를 $W^Q\in R^{d_{model}\times d_k}, W^K\in R^{d_{model}\times d_k}, W^V\in R^{d_{model}\times d_v}$ 와의 행렬 곱으로 구합니다. $d_k, d_v$는 추후 multi-head attention 을 위해 head 개수 $h=8$ 을 $d_{model}=512$ 에서 나눠준 64를 사용합니다.

두 번째 스텝은 query / key 벡터를 곱하여 (dot product) attention score 를 계산합니다. Figure 7에서와 같이 "Thinking" 이라는 단어에 대해 self-attention 을 계산하려 한다면 "Thinking" 의 query $q_1$에 대해 각 위치의 key 벡터를 곱해줌으로써 각 위치별 attention score 를 구하고 이 score 는 해당 위치의 단어가 다른 위치의 단어에 얼마만큼 집중할 것인지를 나타냅니다.
세 번째 스텝은 dot-product 로 계산한 attention score 를 $\sqrt{d_k}$로 나누어주고 softmax 함수를 취해 확률 형태로 나타냅니다. 마지막으로 확률 형태로 나타내어진 softmax score 를 weight 로 하여 각 위치의 value 벡터와 weighted sum 을 계산합니다. 최종적으로 Figure 7의 마지막 $z$가 특정 위치에서의 self-attention score 라고 볼 수 있습니다.

Figure 7은 한 위치의 벡터에 대해 self-attention 연산을 수행한 것이고 이를 입력 문장 전체에 대해 행렬 형태로 나타내면 Figure 8과 같습니다.

Attention score 를 계산하는 방식에는 크게 additive / dot-product 두 가지가 있습니다. 논문에서는 dot-product attention 이 최적화된 행렬곱연산을 이용할 수 있기에 additive attention 에 비해 더 빠르고 공간복잡도가 적어 dot-product 로 attention score 를 계산합니다. 또한, $d_k$가 커질수록 dot-product 의 결과가 커지므로 softmax 함수의 특성 상 특정 노드의 값이 1에 가까워지는 현상이 발생합니다. ($d_k$가 커질수록 dot-product 의 결과가 커지는 이유는 $q, k$가 평균이 0, 분산이 1인 확률변수라 가정하면 $q\cdot k=\sum_{i=1}^{d_k}q_i k_i$는 평균이 0, 분산이 $d_k$가 되기 때문입니다. 즉, 결과값이 커질 확률이 높아지는 것이죠.)
Softmax 결과 특정 노드의 값이 1에 가까워지면 softmax gradient 로 인해 초기 학습에 문제가 발생할 여지가 있습니다. Equation 1에서 볼 수 있듯이 softmax 의 결과값 $y_i$가 한 노드는 거의 1에 가깝고 나머지 노드는 거의 0에 가깝다면 gradient 자체가 매우 작아지게 됩니다. 따라서 초기 학습이 잘 진행되지 않을 가능성이 높으므로 dot-product 연산시 softmax 함수 전에 $\sqrt{d_k}$를 나눠주는 scaling 작업을 해주게 됩니다.
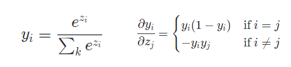
Multi-head attention
Transformer 에서는 단순히 하나의 attention 을 수행하는 것이 아닌 $h=8$ 번만큼의 attention 을 독립적으로 수행하는 multi-head attention 을 사용합니다. 각 head 별로 $W^Q, W^V, W^K$가 존재하여 Figure 9와 같이 병렬적으로 attention 을 수행하는 것이죠. Figure 9와 같이 각 head 별로 추출된 $d_v$ 벡터를 이어붙이고 (concat) 이를 $W^O \in R^{hd_v \times d_{model}}$ 에 곱한 값을 self-attention sublayer 의 최종 결과값으로 사용합니다.

Single attention 에 비해 mutli-head attention 이 지니는 장점이 무엇일까요? 먼저 해당 시퀀스의 특정 위치에 대해 다른 위치에 대한 attention 능력을 향상시킬 수 있습니다. 예를 들어 head 0의 $z_1$이 자기 자신의 위치에만 지나치게 집중하게끔 되버린다면 우리가 고려하고 싶은 다른 위치와의 연관성을 모델링할 수 없겠죠. Multi-head attention 을 사용함으로써 모델이 각 위치별로 여러개의 representation subspace 로부터 각기 다른 attention 정보를 추출해 종합할 수 있게 됩니다. 실제로 각 head 별로 attention score 를 뽑아보면 Figure 10과 같이 각기 다른 위치에 집중하는 양상을 보입니다.

Self-attention sublayer 의 전체적인 과정을 그림으로 표현하면 Figure 11과 같습니다.

Applications of attention in Transformer
Transformer 에서는 multi-head attention 을 다음과 같은 3가지 구성요소에 사용합니다.
- Decoder 의 encoder-decoder attention layer 에 사용합니다. Query 는 직전 decoder layer 로부터 받은 출력으로 사용하고 key, value 는 encoder 의 출력을 사용합니다. 이 과정을 통해 decoder 의 각 위치가 입력 시퀀스의 모든 위치에 대해 attention 을 수행할 수 있습니다.
- Encoder 의 self-attention layer 에 사용합니다. Query/key/value 모두 직전 encoder layer 로부터 받은 출력으로 계산되고 encoder 의 각 위치가 입력 시퀀스의 모든 위치에 대해 attention 을 수행합니다.
- 마찬가지로 decoder 의 self-attention layer 에 사용합니다. 다만 decoder 에서는 현재 입력은 미래가 아닌 과거로부터만 영향을 받는다는 causality / auto-regressive 를 유지하기 위해 softmax 함수에 들어가기 전의 dot-product 수행 시 해당 위치에 대한 미래 부분을 $-\infty$로 마스킹하여 해당 부분에 대해 attention 이 수행되지 못하게 합니다.
Other details
먼저 전체적인 Transformer 구조는 Figure 12와 같습니다. 입력, 출력 시퀀스에 대해 임베딩을 수행하고 encoder, decoder layer 가 $N=6$ 회만큼 동일하게 반복됩니다. 특히, 각 sublayer 마다 residual connection 을 수행하고 layer normalization 을 적용합니다. 따라서 각 sublayer 의 최종 줄력은 입력 $x$에 대해 $LayerNorm(x+Sublayer(x))$ 가 됩니다.

Position-wise feed-forward networks
Encoder / decoder 에서 self-attention 을 수행하고 feed-forward networks 를 거치게 됩니다. 각 위치마다 같은 feed-forward networks 가 수행되며 두 개의 선형 변환과 중간의 ReLU activation 으로 구성되어 있습니다.
$FFN(x) = max(0, xW_1 + b_1)W_2 + b_2$
Feed forward networks 는 모든 위치에 동일하게 적용되나 각 layer 마다 다른 파라미터를 사용합니다. 입력과 출력의 차원은 마찬가지로 $d_{model}=512$ 를 사용하며, 중간 차원은 $d_{ff}=2048$ 을 사용합니다.
Feed-forward networks 는 encoder / decoder 전부에 대해서 self-attention layer 이후에 적용됩니다. 즉, multi-head attention 으로 뽑아낸 각 위치 별 컨텍스트를 커플링해서 feature 차원으로 다시 프로젝션하는 역할을 맡는 것이라 생각할 수 있습니다.
Embedding and softmax
입력과 출력 시퀀스를 $d_{model}$ 차원을 가진 벡터로 변환하기 위해 임베딩을 수행하며 입력, 출력 시퀀스에 대해 같은 임베딩 행렬을 사용합니다. 또한, 출력 시에는 최종 결과물의 벡터를 우리가 아는 단어로 변환시켜야 하는데 Figure 13과 같이 각 위치마다 vocabulariy 사이즈만큼 선형변환 후 softmax 를 사용하며 각 위치마다 동일한 선형 파라미터를 사용합니다.

Positional encoding
Transformer 에서는 recurrence, convolution 이 존재하지 않기 때문에 시퀀스의 각 위치의 순서를 알려주는 positional 정보가 필요합니다. 따라서 임베딩 이후에 positional encoding 벡터를 더해줌으로써 모델이 각 단어의 위치와 시퀀스 내의 다른 단어 간의 위치 차이에 따른 정보를 알 수 있게 해줍니다. Positional encoding 은 마찬가지로 $d_{model}$ 차원의 벡터이며 Transformer 에서는 Equation 2와 같은 사인, 코사인 함수를 사용합니다.
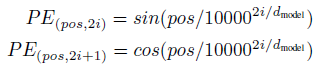
Equation 2의 $pos$는 위치이고 $i$는 차원입니다. 따라서 짝수 차원은 사인함수, 홀수 차원은 코사인 함수로 positional encoding 을 수행하고 주기는 $2\pi$ 부터 $10000\cdot 2\pi$ 까지 다양하게 존재합니다. Positional encoding 은 이 방법 이외에도 학습을 하거나 다른 방법이 존재하지만 Transformer 에서 sinusoidal 함수를 사용한 이유는 본 적이 없는 긴 길이에 시퀀스에 대해서도 쉽게 positoinal encoding 을 생성할 수 있기 때문입니다.
Decoder operation
Decoder 가 동작을 수행하기 위해서는 Figure 14와 같이 encoder 가 먼저 입력 시퀀스를 처리하고 decoder 에 전달하기 위한 $K, V$ 를 생성해야 합니다. Encoder 로부터 추출된 입력 시퀀스의 representation $K, V$는 decoder layer 의 encoder-decoder attention sublayer 에 전달됩니다.

이후에는 Figure 15와 같이 decoder 가 매 스텝마다 출력을 생성하고 출력을 완료했다는 신호인 <end of sentence> 심볼이 출력될때까지 반복됩니다. 중요한 점은 Figure 15에서는 decoder 에 들어가는 출력 시퀀스와 최종 아웃풋의 순서가 같게 나와있지만 현재 스텝의 아웃풋이 다음 스텝의 입력으로 들어가므로 decoder 의 입력은 한 칸씩 오른쪽으로 shift 된 값이 들어가게 됩니다. (Figure 12의 shifted right) 또한, 위에서도 언급했듯이 현재 위치에서 이전 위치에 대해서만 attention 을 수행해야 하므로 현재 이후의 위치에 대해서는 dot product 결과에 $-\infty$를 가해주는 마스킹을 수행합니다.

Why self-attention
Table 1은 self-attention 이 convolution, recurrent 에 비해 1) complexity per layer, 2) sequential operation, 3) maximum path length 3가지 측면에서 어떤 장점이 있는지 분석한 표입니다. Sequential operation 은 병렬화가 얼마나 가능한지를 측정하기 위한 지표이고 시퀀스 모델링에서 가장 중요한 점은 long-term 의존성을 모델링 하는 것이기 때문에 입력, 출력 위치간의 거리가 짧을 수록 학습에 더 용이하므로 maximum path length 를 분석합니다.

먼저 self-attention 은 $QK^T$ 부분이 $O(n^2\cdot d)$ 만큼 소요되고 각 위치별로 병렬적으로 attention 이 계산되어 sequential operation, maximum path length 가 모두 $O(1)$ 이 소요됩니다. 반면, recurrent 는 $O(n\cdot d^2)$ 의 complexity 가 소요되고 모든 스텝에 대해 sequential 하게 계산되어야 하므로 sequential operation, maximum path length 가 $O(n)$이 소요됩니다. 따라서, self-attention 은 일반적으로 $n < d$이므로 recurrent 보다 complexity 가 적습니다. 1차원 convolution 의 경우 $k < n$ 이므로 입력, 출력의 모든 위치를 연결하지는 못합니다. 따라서 dilated convolution 을 사용한다면 모든 위치를 다 연결하기 위해 $O(log_k (n))$개의 층이 필요하게 되며 이만큼 maximum path length 에 소요됩니다.
또한, convolution 은 kernel 의 존재로 인해 recurrent 에 비해 연산량이 비싸게 되는데, separable convolution 을 사용하여 complexity 를 $O(k\cdot n\cdot d+n\cdot d^2)$로 줄인다고 하더라도 Transformer 에서 self-attention, feed forward 연산량을 합쳤을 때와 complexity 가 같아집니다. 즉, self-attention 이 기존의 recurrent, convolution 에 비해 시퀀스 모델링에 강점이 뚜렷합니다. 더불어 self-attention 을 통해 각 위치별로 어떤 부분에 attention 이 많이 가해졌는지 볼 수 있는 해석 또한 부가적으로 제공하는 장점이 있습니다.
참조
다음 포스트
'Machine Learning Models > Transformer' 카테고리의 다른 글
| Vision Transformer (3) - Attention Map (3) | 2021.06.17 |
|---|---|
| Vision Transformer (2) (0) | 2021.06.16 |
| Vision Transformer (1) (3) | 2021.06.16 |
| Transformer Positional Encoding (6) | 2021.06.16 |
| Transformer 구현 (0) | 2021.05.27 |



