파이썬은 인터프리터 언어로서 C/C++/Fortran 과 같은 컴파일 언어에 비해 느리지만, 파이썬 코드를 LLVM 컴파일러를 이용해 머신 코드로 바꾸어 수치연산을 가속화해주는 Numba 컴파일러가 존재합니다.Numba는 수치 계산에 초점을 맞춘 파이썬을 위한 오픈 소스 JIT (Just-In Time) 컴파일러로 2012년 컨티넘 애널리틱스 (현재 아나콘다) 에서 처음 만들어졌습니다. Numba 라이브러리의 주요 특징으로는,
- 전체 애플리케이션, 프로그램이 아닌 @jit, @njit 데코레이터로 장식된 함수에 대해서만 별도로 컴파일합니다. 파이썬은 보통 파이썬 인터프리터 CPython 을 사용하는데, Numba 는 별도의 인터프리터를 사용하지 않고 최적화된 별도의 빠른 함수를 만들어줍니다.
- 함수에는 입력 (아규먼트), 출력 (리턴)이 존재하는데 Numba 는 특정 수치형 데이터 타입에 (int, float, complex) 대해서 빠른 연산을 제공합니다. 따라서 numpy array 와 일반적으로 같이 사용합니다.
- 함수가 처음 호출되었을 때 컴파일합니다. (Just In Time, JIT) 그 이후로 타입이 같은 인자를 전달해 함수를 실행하면 컴파일된 버전을 사용해 원래 버전보다 빠르게 작동합니다.
- Numba는 파이썬 뿐만 아니라 넘파이를 인식해서 넘파이를 사용하는 코드도 컴파일합니다. 하지만 완전한 컴파일러는 아니어서 파이썬과 넘파이의 일부분만 컴파일할 수 있습니다.
- Numba는 내부적으로 LLVM 프로젝트에 의존합니다. LLVM (https://llvm.org/) 프로젝트는 재사용할 수 있고 모듈화된 컴파일러와 툴체인 기술의 모음입니다.
Numba 라이브러리의 동작 과정은 Figure 1과 같습니다. Numba 라이브러리의 jit 모듈을 가속화하고자 하는 함수에 decorating 하면 함수의 아규먼트의 타입을 파악하고 (type inference), LLVM 컴파일러의 입력으로 변환해주는 과정을 (Lowering) 거쳐 머신 코드로 컴파일하게 됩니다.

Examples
Standard deviation
입력으로 주어진 배열에 대해 표준편차를 (standard deviation) 계산해보도록 하겠습니다. Numba 라이브러리 사용에 따른 속도 측정을 하기 위해 for 루프를 두 번 사용했습니다.
def std(xs):
# compute the mean
mean = 0
for x in xs:
mean += x
mean /= len(xs)
# compute the variance
ms = 0
for x in xs:
ms += (x-mean)**2
variance = ms / len(xs)
std = math.sqrt(variance)
return std
import numpy as np
a = np.random.normal(0, 1, 10000000)Jupyter notebook 이나 리눅스의 CLI 상의 "timeit" 함수를 이용하여 함수가 실행되는 속도를 측정할 수 있습니다.
>>> %timeit std(a)
1 loop, best of 5: 8.34 s per loopNumba 라이브러리의 "njit" 데코레이터를 호출하여 "std" 함수를 감싼 이후에 속도를 측정해보겠습니다.
from numba import njit
c_std = njit(std)
>>> %timeit c_std(a)
10 loops, best of 5: 32.3 ms per loop대략 200배 정도 빨라진 것을 확인할 수 있습니다. 물론 "std" 함수에 numpy 배열을 직접 전달하는 것이 아니라 numpy builtin 함수를 이용해 계산하면 이에 준하는 결과를 얻을 수 있습니다. 더 복잡한 경우를 알아보겠습니다.
Calculation of pi
$\pi$는 Figure 2에서 Monte-Carlo 방법으로 구할 수 있습니다. 원면적 대비 사각형면적의 비율 $r$은 $r=\frac{A_c}{A_s}=\frac{\pi R^2}{L^2}=\frac{\pi}{4}$ 이므로 $r$에 4를 곱하면 $\pi$를 대략적으로 추정할 수 있습니다. 따라서 [[-1,1],[-1,1]] 사이의 uniform 분포에서 많은 점을 추출하여 추출한 점에서 원 안에 떨어지는 점의 개수로 $r$을 추정함으로써 $\pi$를 추정할 수 있습니다. 당연히 추출한 점이 많을수록 $\pi$가 정확해지겠죠.

import random
def pi(npoints):
n_in_circle = 0
for i in range(npoints):
x = random.random()
y = random.random()
if (x**2+y**2 < 1):
n_in_circle += 1
return 4*n_in_circle / npoints
>>> npoints = [10, 100, 10000, int(10e6)]
>>> for number in npoints:
>>> print(pi(number))
3.6
3.24
3.1524
3.1411972천만 개의 포인트를 샘플링해서 $\pi$를 계산할 떄의 소요시간을 측정해보면 다음과 같습니다.
>>> %timeit pi(10000000)
1 loop, best of 5: 4.41 s per loop이 알고리즘은 간단히 $O(N)$의 시간복잡도가 소요됩니다. 따라서 샘플링할 포인트를 10억개로 늘리면 최소 분단위 이상의 시간이 소요됩니다. Numba 라이브러리의 "njit" 으로 "pi" 함수를 데코레이팅 한 이후에 계산해보면 대략 10초의 시간이 소요됩니다.
@njit
def fast_pi(npoints):
n_in_circle = 0
for i in range(npoints):
x = random.random()
y = random.random()
if (x**2+y**2 < 1):
n_in_circle += 1
return 4*n_in_circle / npoints
>>> %timeit fast_pi(int(1e9))
1 loop, best of 5: 12.5 s per loopFinding the closest two points
그렇다면 임의의 수많은 점들에 대해 가장 가까운 2개의 점을 찾는 알고리즘에 대해서는 어떨까요? Brute-force 방식으로 계산하면 $O(N^2)$ 시간복잡도가 소요됩니다. 2000개의 포인트에 대해서 속도를 측정하면 다음과 같습니다.
import math
def closest(points):
'''Find the two closest points in an array of points in 2D.
Returns the two points, and the distance between them'''
mindist2 = 999999.
mdp1, mdp2 = None, None
for i in range(len(points)):
p1 = points[i]
x1, y1 = p1
for j in range(i+1, len(points)):
p2 = points[j]
x2, y2 = p2
dist2 = (x1-x2)**2 + (y1-y2)**2
if dist2 < mindist2:
# squared distance is improved,
# keep it, as well as the two
# corresponding points
mindist2 = dist2
mdp1, mdp2 = p1,p2
return mdp1, mdp2, math.sqrt(mindist2)
>>> points = np.random.uniform((-1,-1), (1,1), (2000,2))
>>> %timeit closest(points)
1 loop, best of 5: 4.61 s per loop이를 마찬가지로 "njit" 으로 데코레이팅 한 이후 측정하면 100배 이상 빨라집니다.
from numba import njit
c_closest = njit(closest)
>>> %timeit c_closest(points)
1 loop, best of 5: 38.1 ms per loop
jit, njit
Numba 라이브리러에서는 "jit" 혹은 "njit" 을 이용하여 함수를 데코레이팅 할 수 있습니다. 위의 예제에서는 "njit" 을 사용했지만 가장 기본이 되는 데코레이터는 "jit" 으로 "njit" 은 "jit(nopython=True)" 와 같습니다. Numba 에서는 "object mode" / "nopython mode" 가 존재하는데 "nopython mode" 는 CPython 인터프리터를 사용하지 않겠다는 것으로 가장 최적의 컴파일 코드를 제공합니다. 하지만 이것은 int, float, complex 와 같은 지정된 타입에 대해서만 동작합니다. 예를 들어 다음 예와 같이 딕셔너리 형태에 대해서는 "nopython mode" 가 동작하지 않습니다.
@jit(nopython=True)
def cannot_compile(x):
return x['key']
cannot_compile(dict(key='value'))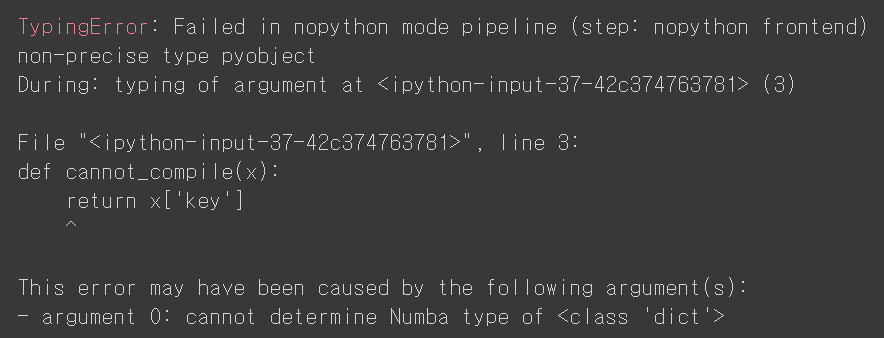
"jit" 에 "nopython" 아규먼트를 지정하지 않으면 디폴트로 "object mode" 로 컴파일됩니다. 이것은 모든 형태의 파이썬 객체를 컴파일할 수 있는 모드이지만 수치형 타입이 아닌 데이터에 대해서 최적의 속도를 보장하지 않습니다. 다만, "nopython" 을 지정하지 않더라도 "loop-jitting" 이라는 컴파일 특성에 의해 수치형 타입에 대해서는 자동으로 "nopython mode" 로 컴파일됩니다.
또한, "jit" 을 이용하면 다음과 같이 함수의 아규먼트, 출력의 타입을 미리 지정할 수 있어 Figure 1의 type inference 단계를 건너뛸 수 있습니다. 미리 지정하지 않는 경우에는 첫번째 함수 실행때까지 컴파일이 연기됩니다.
from numba import jit
@jit('Tuple((float64[:], float64[:], float64))(float64[:,:])', nopython=True)
def c_closest(points):
mindist2 = 999999.
mdp1, mdp2 = None, None
for i in range(len(points)):
p1 = points[i]
x1, y1 = p1
for j in range(i+1, len(points)):
p2 = points[j]
x2, y2 = p2
dist2 = (x1-x2)**2 + (y1-y2)**2
if dist2 < mindist2:
mindist2 = dist2
mdp1 = p1
mdp2 = p2
return mdp1, mdp2, math.sqrt(mindist2)
참조
- https://thedatafrog.com/en/articles/make-python-fast-numba/
- https://github.com/ContinuumIO/gtc2018-numba/blob/master/1%20-%20Numba%20Basics.ipynb
- http://numba.pydata.org/numba-doc/latest/glossary.html#term-object-mode
- https://gurujung.github.io/dev/numba_user_jit/
'Computer > Python' 카테고리의 다른 글
| GIL (Global Interpreter Lock), Multi-Threading (0) | 2021.06.20 |
|---|---|
| 제너레이터와 yield (1) (0) | 2021.06.14 |
| Pycharm - Python Interpreter (0) | 2021.05.11 |
| 예외 처리에서의 동작 수행 - try/except/else/finally (0) | 2021.05.04 |
| Mutable Default Arguments (0) | 2021.04.29 |



