KMeans는 대표적인 군집화 알고리즘으로 간단한 특성으로 인해 온사이트 인터뷰나 코딩 테스트에서 스크래치부터 구현해보라는 문제가 가끔씩 출제됩니다. 이번 포스트에서는 scikit-learn, numpy 같은 외부 라이브러리 없이 파이썬의 내장 함수와 라이브러리만으로 KMeans 알고리즘을 구현해보도록 하겠습니다. 군집화할 데이터는 10000개의 16차원 벡터라 가정하면 16개의 실수 요소를 가진 리스트 10000개를 요소로 가진 리스트가 됩니다.
Utility functions
Euclidean distance
Distance metric으로 Euclidean distance를 계산하는 함수를 구현합니다. 입력으로 같은 길이의 리스트 2개를 받고 각 요소 별 차이의 제곱을 모두 더한 후 math 라이브러리의 sqrt 함수를 이용해 루트를 적용합니다.
import math
def calc_dist(A, B):
'''
Calculate Euclidean distance
'''
assert len(A) == len(B)
sum = 0
for a, b in zip(A, B):
sum += (a - b)**2
return math.sqrt(sum)
test_a = [1,2,3,4]
test_b = [4,3,2,1]
calc_dist(test_a, test_b)
Cluster centroid
KMeans는 매 스텝마다 업데이트된 클러스터를 기반으로 각 클러스터의 중심을 새롭게 구합니다. 입력으로는 각 클러스터에 할당된 벡터의 리스트가 되고 벡터 요소 별로 모두 더한뒤 개수만큼 나누어주어 각 차원 별 평균을 구해줍니다.
def calc_vector_mean(array):
summation = [0] * len(array[0])
for row in array:
for d in range(len(row)):
summation[d] += row[d]
for s in range(len(summation)):
summation[s] = summation[s] / len(array)
return summation
test_array = [[1,2,3,4,5],
[2,3,4,5,6],
[3,4,5,6,7]]
calc_vector_mean(test_array)
Update tolerance
이 함수는 KMeans 알고리즘 동작 시 각 클러스터 중심이 미리 정의한 임계치보다 작게 업데이트 된다면 알고리즘 수행을 멈추게 되는데, 전 스텝의 클러스터 중심과 현 스텝의 클러스터 중심의 Euclidean distance로 정의합니다. 따라서 위에서 정의한 "calc_dist" 함수를 사용합니다.
def calc_diff(A, B):
'''
Calculate Euclidean distance between two arrays (A, B)
Arguments:
- A, B: Arrays with same shape
Returns:
- Euclidean scalar value
'''
tol = 0
for a, b in zip(A, B):
tol += calc_dist(a, b)
return tol
prev_centroids = [[1,2,3,4,5],
[10,9,8,7,6]]
pres_centroids = [[1.1, 2.1, 2.9, 3.9, 5.1],
[10,9.1,8.9,6.9,5.1]]
calc_diff(prev_centroids, pres_centroids)
KMeans
KMeans 알고리즘을 구현합니다. Scikit-learn 스타일로 생성자 함수에서 클러스터 개수, 최대 스텝 횟수, 알고리즘을 계속 수행하기 위한 클러스터 중심 업데이트 임계치를 정의합니다.
class Clustering(object):
def __init__(self, k, max_iter=10, tol=1e-4):
'''
Arguments:
- k: Number of clusters
- max_iter: Maximum number of iteration
- tol: Update tolerance, if centroids update is smaller than this value, fitting will stop
'''
self.k = k
self.max_iter = max_iter
self.tol = tol- 클러스터 중심이 tol 인자의 숫자보다 작게 업데이트되면 최대 스텝 횟수에 동작하지 않더라도 알고리즘을 종료합니다.
Initialization
군집의 초기 중심을 선언합니다. 원래의 KMeans는 랜덤하게 초기 중심점을 잡지만 이럴 경우 초기화 상황에 따라 수렴이 매우 느려질 수 있으므로 각 군집 중심을 최대한 멀리 잡는 KMeans++를 사용합니다. 입력으로는 전체 데이터를 받습니다.
def random_init(self, array):
'''
K-Means++ init
'''
M = [] # Indices of initial points
indices = []
i = random.randint(0, len(array))
M.append(array[i])
indices.append(i)
while len(M) < self.k:
max_dist = -float('inf')
max_index = -1
for i in range(len(array)):
avg_dist = 0
if i in indices:
continue
for j in range(len(M)):
dist = calc_dist(array[i], array[j])
avg_dist += dist
avg_dist /= len(M)
if max_dist < avg_dist:
max_dist = avg_dist
max_index = i
## Add init point which has largest average distance in M
#print(max_index)
#print(max_dist)
M.append(array[max_index])
indices.append(max_index)
return M- 전체 데이터 중에서 랜덤하게 임의의 초기값을 하나 잡고 군집 중심 리스트 (M)에 담습니다.
- 이후에는 전체 데이터에 대해 각각 M에 속한 중심값과의 평균 거리를 계산하고 평균 거리가 가장 큰 데이터를 M에 추가합니다.
- 전체 데이터에 반복 시 M에 속한 데이터에 대해서는 거리계산을 할 필요가 없으므로 continue 키워드를 사용하여 다음 반복문을 수행합니다.
Fit
KMeans 훈련 코드를 작성합니다. 지정한 최대 스텝 횟수에 맞게 1) 군집 재할당, 2) 군집 중심 계산을 반복합니다. 지정한 임계치보다 군집 중심이 작게 업데이트되면 훈련을 종료합니다.
def fit(self, X):
'''
Arguments:
- X: Array of [10000, 16]
Returns:
- Cluster assignment of each vector, Centroids of cluster
'''
self.centroids = self.random_init(X)
for iter in range(self.max_iter):
print(f'{iter+1} iteration...')
## Assign cluster
self._assign_cluster(X)
## Update centroids
self._update_centroids(X)
if calc_diff(self.prev_centroids, self.centroids) < self.tol:
break
return self.assignments, self.centroids데이터 별로 군집 번호를 할당하는 "_assign_cluster" 함수를 구현합니다. 데이터 별로 거리가 가장 짧은 군집 중심에 대해 군집을 할당합니다.
def _assign_cluster(self, X):
self.assignments = []
for d in X:
min_dist = float('inf')
min_index = -1
for i, centroid in enumerate(self.centroids):
dist = calc_dist(d, centroid)
if dist < min_dist:
min_dist = dist
min_index = i
self.assignments.append(min_index)다음으로 할당된 군집에 대해 군집 중심을 업데이트하는 "_update_centroids" 함수를 작성합니다. 주의할 점은 데이터의 분포나 군집 수에 따라서 우리가 지정한 군집 수보다 적은 군집이 할당되는 경우가 생길 수 있다는 점입니다. 즉, 특정 군집에 대해 할당된 데이터가 아예 없는 경우가 생길 수 있다는 것이죠. 다음 그림과 같은 상황에서,
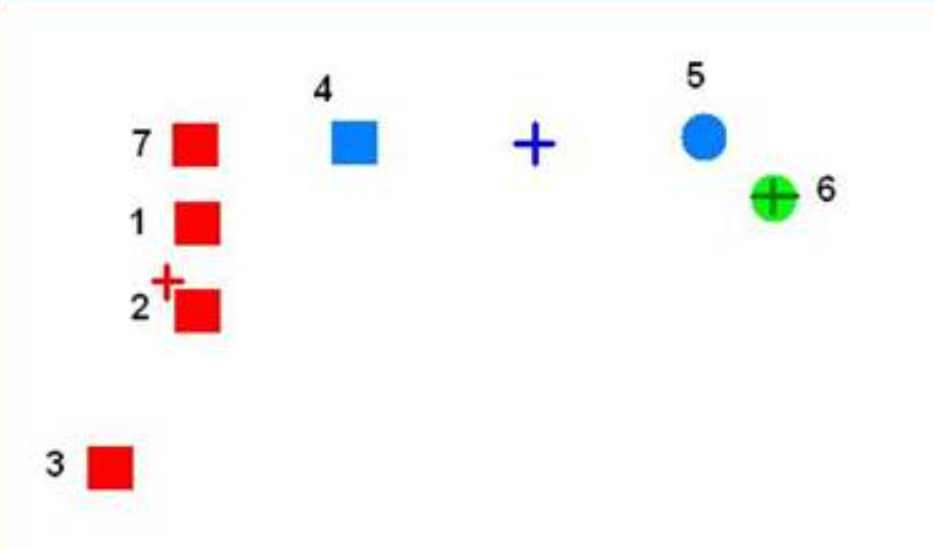
알고리즘을 진행하면 4번 데이터는 빨간색 군집, 5번 데이터는 초록색 군집에 가깝기 때문에 다음 그림과 같이 파란색 군집에는 데이터가 아예 할당되지 않습니다.
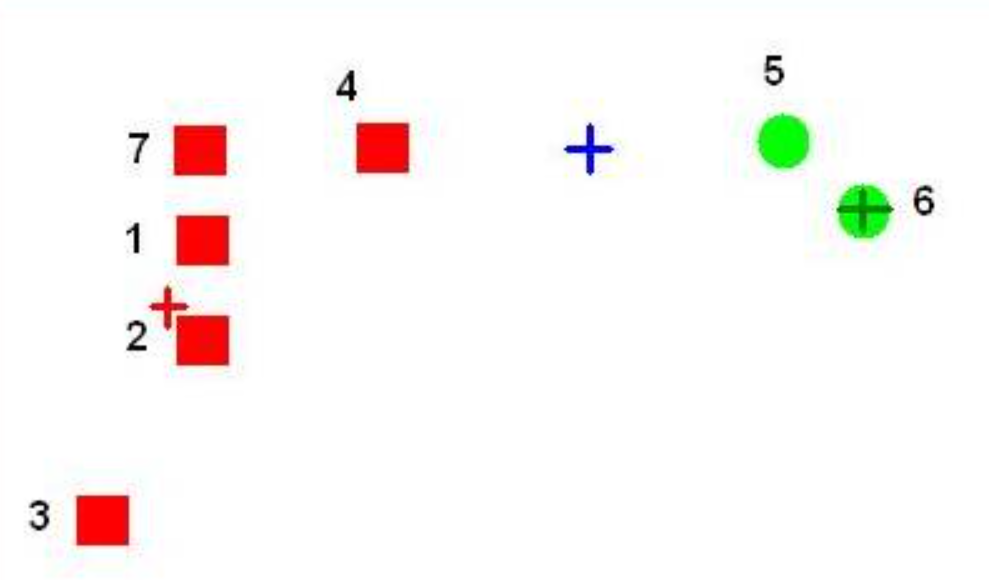
이러한 경우에는 가장 간단하게는 전체 데이터에서 랜덤하게 데이터를 하나 샘플링해서 군집에 데이터를 하나 강제로 할당해 주거나 SSE (Sum of Squared Error)가 가장 큰 군집에서 데이터를 하나 뽑아주는 방법이 있습니다. 물론 가장 좋은 방법은 군집 개수를 줄이는 것이겠죠. 코드는 다음과 같습니다.
def _update_centroids(self, X):
self.prev_centroids = copy.deepcopy(self.centroids)
for i in range(self.k):
## Filter data with 'i' cluster
data_indices = list(filter(lambda x: self.assignments[x] == i, range(len(self.assignments))))
## If there isn't any data points to cluster
## Assign random point from data
if len(data_indices) == 0:
r = random.randint(0, len(X))
self.centroids[i] = X[r]
continue
cluster_data = []
for index in data_indices:
cluster_data.append(X[index])
self.centroids[i] = calc_vector_mean(cluster_data)
참조
'Computer > Coding Test' 카테고리의 다른 글
| 파이썬으로 행렬 구현하기 (2) (0) | 2022.02.19 |
|---|---|
| 파이썬으로 행렬 구현하기 (1) (0) | 2022.02.19 |
| 코딩테스트 문제 (28) - 정렬 리스트 병합하기 (0) | 2021.06.20 |
| 코딩테스트 문제 (27) - 리스트에서 부분집합 출력하기 (0) | 2021.06.11 |
| 코딩테스트 문제 (26) - 최대 공약수, 최소 공배수 (0) | 2021.03.10 |

