삽입 정렬은 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 원소들과 비교하여 자신의 위치를 찾아가는 정렬방법입니다. for 문을 통해 배열의 원소를 순회하면서 해당 인덱스의 원소가 찾아갈 위치를 앞부분의 어디에 삽입할 것인가를 찾는 알고리즘인데요, 특이하게도 삽입 정렬은 배열의 두 번째 인덱스부터 루프를 시작합니다. 배열 [8,5,6,2,4] 예를 들어 살펴볼까요?
Example
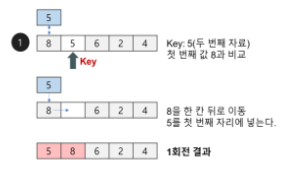
1. 첫 번째 스텝입니다. 두 번째 인덱스인 5부터 for 루프를 시작합니다. 두 번째 인덱스 기준에서는 앞선 인덱스가 첫 번째 인덱스밖에 없으니 첫 번째 원소인 8과 비교를 하고 8이 5보다 크니 둘의 위치를 바꿔줍니다.
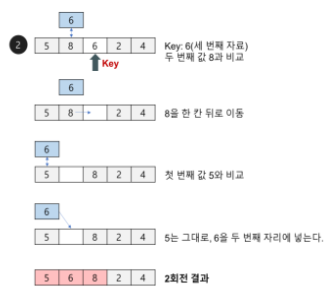
2. 두 번째 스텝입니다. 세 번째 인덱스인 6을 기준으로 앞서 첫 번째 스텝에서 정렬되었던 배열에 대해 비교를 시작합니다. 앞서 두 번째 인덱스로 옮겨졌던 8이 6보다 크므로 8과 6이 스왑되지만 5는 6보다 작으므로 6의 위치는 두 번째 인덱스가 됩니다.
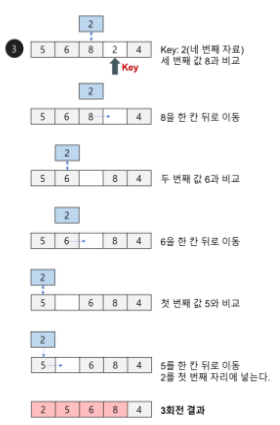
3. 세 번째 스텝입니다. 네 번째 인덱스인 2를 기준으로 앞선 배열 [5,6,8] 과 비교를 시작합니다. 과정은 똑같습니다. 2가 왼쪽으로 옮겨가면서 자기보다 크면 스왑을 작으면 그 자리에서 멈춥니다. 결과적으로 이번 스텝에서는 2가 5,6,8 보다 작으니 맨 앞에 위치하게 됩니다.
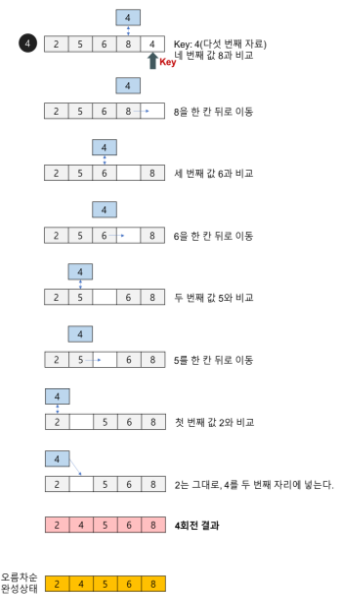
4. 마지막 스텝입니다. 이 부분도 마찬가지로 돌아갑니다. 앞서 정렬된 배열 [2,5,6,8]에 대해 4가 왼쪽으로 움직이면서 더 작아지지 않는 선에서 이동을 멈추고 그 자리에 삽입되게 됩니다. 삽입정렬 특성 상 for 루프를 돌면서 해당 인덱스의 앞선 인덱스들은 이미 정렬이 되었기 때문에 이렇게 단순 비교를 통해 옮기는 것이 가능합니다.
파이썬 코드
def typing import List
def insertion_sort(List: array) -> List:
for i in range(1, len(array)): # for 루프는 두 번째 인덱스부터 시작
for j in range(i, 0, -1): # i 보다 앞선 인덱스에 대해 비교
## Swap
if array[j] < array[j-1]:
array[j], array[j-1] = array[j-1], array[j]
else: # 정렬이 다 되었으므로 break
break
return array
시간 복잡도
삽입 정렬도 제자리 정렬 (in-place) 이므로 공간 복잡도는 고려할 필요가 없습니다. 그럼 삽입정렬의 시간 복잡도는 어떻게 될까요? 기본적으로 for 루프가 두 번 들어가니 $O(n^2)$ 일 것으로 짐작할 수 있습니다. 그렇다면 항상 $O(n^2)$가 될까요? 시간 복잡도 계산은 입력의 조건에 따라 최선의 경우, 최악의 경우 로 나누어 생각할 수 있습니다. 먼저, 최악의 경우는 어떤 케이스가 될까요?
최악의 경우
최악의 경우는 내부 루프에서 매번 비교하는 케이스가 될 겁니다. 내림차순으로 정렬된 배열을 삽입정렬을 이용해 오름차순으로 배열한다고 생각해보면, 두 번째 루프 안에서도 매번 비교하며 스왑할테니 $O(n^2)$이 될 겁니다.
최선의 경우
이미 오름차순으로 정렬된 배열이 있다고 가정해보면 이미 정렬되어 있으므로 내부 루프를 다 순회하지 않고 break 문에 의해 내부 루프가 바로 끝나게 됩니다. 따라서 최선의 경우에는 $O(n)$이 되겠네요.
홍머스 정리
- 이미 어느 정도 정렬된 배열에 대해서 매우 빠르다.
- 두 번째 인덱스부터 for loop
참조
- gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
- www.youtube.com/watch?v=DRkL5EBZ7KY&list=PLVsNizTWUw7H9_of5YCB0FmsSc-K44y81&index=22
'Theory > Algorithms' 카테고리의 다른 글
| 병합 정렬 / 합병 정렬 (Merge Sort) (0) | 2021.02.22 |
|---|---|
| 계수 정렬 (Counting Sort) (0) | 2021.02.21 |
| 퀵 정렬 (Quick Sort) (0) | 2021.02.21 |
| 버블 정렬 (Bubble Sort) (0) | 2021.02.20 |
| 선택 정렬 (Selection Sort) (0) | 2021.02.20 |

