이 논문은 classification 기반의 이상 탐지를 수행한 GEOM (Geometric-transformation classification) 을 확장하여 이미지 이외의 tabular 등의 다른 데이터 타입에도 적용 가능한 이상 탐지 알고리즘을 (GOAD) 제안한 논문입니다.
훈련 데이터에 정상 데이터만 포함된 semi-supervised 시나리오를 가정하였고 open-set classification 에서 영감을 받아 inter-class separation (각 클래스 간의 거리)은 늘리고 intra-class separation (한 클래스 안의 거리) 줄어들도록 GEOM 알고리즘을 개선했습니다. 또한, 이미지가 아닌 데이터에 대해서도 일반화가 가능하도록 기존의 기하학적인 transformation을 affine transformation으로 확장하였습니다.
GOAD
Previous approach
모든 데이터가 존재하는 space를 $\mathcal{X}$, 정상 데이터가 존재하는 space를 $X$, 비정상 데이터는 $\mathcal{X}\backslash X$에 존재한다고 했을 때, 이상 탐지는 $x\in X$에 대해 1, $x\in \mathcal{X}\backslash X$에 대해 0을 도출하는 classifier을 구축하는 것입니다.
Deep-SVDD의 경우 neural networks를 통해 feature space로 데이터를 매핑하고 $c_0$를 중심으로 한 최소한의 hypersphere를 찾는 문제입니다. Hypersphere 밖을 벗어나면 anomaly로 간주됩니다.
GEOM의 경우는 기하학적인 transformation을 모든 이미지에 적용하고 어떤 transformation을 적용했는지 예측하는 classifier를 학습시킵니다. 결과적으로 밑의 수식처럼 변환된 이미지에 대한 transformation의 예측 확률을 추정하게 됩니다. (이를 위해 dirichlet 분포를 사용했습니다) 훈련된 classifier에 대해서 주어진 입력 $x$에 대해 classifier가 anomaly의 transformation을 잘 예측하지 못하는, 즉, $P(m|T(x,m))$이 낮게 되면 높은 anomaly score를 부여합니다.

하지만 문제는 $x\in \mathcal{X}\backslash X$에 대해서는 transform $m$에 대한 subspace $X_{m}$에 대해 $P(T(x,m)\in X_{m})=0$ 이어야 한다는 점입니다. 왜냐하면 정상 데이터만의 변환으로 $X_{m}$을 구성했기 때문이죠. 따라서 classifier의 $P(m'|T(x,m))$은 훈련 데이터의 샘플 $x\in X$에 대해서만 타당하고, 이는 anomaly에 대한 anomaly score 의 변동성이 심한 원인이 됩니다.
이를 해결하기 위한 방법으로는 anomaly 데이터에 대해서도 $X_{m}$을 구성하고 $P(m|T(x,m))=1/M$ 이 되도록 훈련시키면 됩니다. 하지만 이러한 supervision은 얻기가 쉽지 않을 뿐더러 tabular data의 경우 적용하기가 쉽지 않습니다.
Distance-based multiple transformation classification
GEOM의 문제를 해결하면서 다른 데이터 타입에 대한 일반화를 어떻게 달성할 수 있을까요? GOAD는 openset-based classification 방법을 이용합니다. Openset-classification이란 훈련 데이터의 클래스 종류와 테스트 데이터의 클래스 종류가 다른 경우를 말합니다. 보통 이를 위해서 inter-class separation을 최대화하고 intra-class separation을 최소화함으로써 각 클래스의 feature space가 compact하고 서로 멀리 떨어지게 합니다.
GOAD는 GEOM과 같이 $M$개 transformation ($X_1, ..., X_M$)을 생성한 뒤 각 $X_M$이 feature space 상에서 $c_m$을 중심으로 한 sphere를 구성하도록 설계합니다. 또한 $P(T(x,m)) \in X_{m'}$=$\frac{1}{Z}\exp^{-(f(T(x,m))-c_{m'})^2}$ 의 거리 기반으로 parameterize 함으로써 GEOM 때와는 달리 anomaly 의 변환된 이미지가 $X_M$에 존재하지 않는 문제를 고려할 필요가 없어집니다. 결과적으로 transformation $m'$을 예측할 확률은 다음과 같이 주어집니다.

중심 $c_m$은 각 transformation의 average feature가 됩니다. (실제 구현에서의 훈련 때에는 매 iteration 마다 중심을 새롭게 구해주고, inference 시에는 가장 최근의 평균이나 매 iteration마다 누적 평균을 사용합니다)
훈련을 위한 목적 함수로는 transformation 분류를 위한 cross-entropy loss와 intra-class variation을 줄이고 inter-class variation은 늘리는 center triplet loss를 함께 사용합니다. 다음 수식을 보면 해당 transformation $m$에 대해 $c_m$까지의 거리를 줄이면서 다른 중심 $c_m', m\neq m'$과는 멀어지도록 동작하는 것알 알 수 있습니다.

Anomaly 판별을 위한 score로는 위에 정의한 $P(m'|T(x,m))$을 사용합니다. 이때, 어떠한 $c_\tilde{m}$으로부터도 거리가 매우 먼 불확실한 데이터에 대해서는 작은 거리 변화에도 classifier의 분류 결과가 크게 영향을 받게 됩니다. 따라서 어떠한 transformation인지 불분명한 데이터에 대해 같은 확률을 가질 수 있도록 regularizer를 추가합니다.
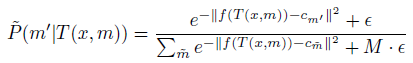
Anomaly score는 모든 데이터에 대해 transformations를 적용하고 각 transformation마다 독립적이라 가정하여 다음과 같이 정의합니다. 비정상일수록 transformation의 중심으로부터 멀어져 score가 높게 나오게 됩니다.

GOAD의 훈련 및 평가 알고리즘은 다음과 같습니다.

Parameterizing the set of transformations
GEOM에서 사용한 geometric transformations 는 공간적인 관계를 가진 이미지에서는 굉장히 잘 동작합니다. 하지만 공간적인 관계가 없는 tabular data에 대해서는 그대로 적용할 수 없습니다. 이를 tabular 데이터에 대해서 일반화하기 위해 transformation의 종류를 다음과 같이 affine transformation으로 일반화합니다.

기하학적인 변환 (회전, translation, flip 등)은 기본적으로 affine transformation에 속합니다. 특히, $W$를 랜덤 distribution에서 샘플링하거나 차원 축소가 가능해집니다.
더불어 특정한 transformation 클래스에 대한 사전 정의가 불가능한 서로 다른 데이터 타입에 대해 일반적으로 적용할 수 있을 뿐만 아니라 분류를 잘 못하도록 방해하는 adversarial example에 대한 방어도 어느 정도 가능해집니다. 만약 transformation 셋이 명확히 정의가 되었다면 adversarial example은 알려진 transformation에 대해 생성이 가능하나 만약 transformation이 명확히 정의되지 않고 랜덤이라면 adversarial attack을 위해서 일반화가 수행되어야 합니다.
정리하면 affine transformation으로 transformation 셋을 이미지가 아닌 데이터에 대해서 일반화하고 transformation 자체를 랜덤하게 샘플링합니다. 실제 구현에서도 tabular data의 경우 랜덤 분포에서 $W$를 샘플링하여 $T(x,m)$을 얻습니다.

Experiments
Image experiments
이미지에 대해서는 CIFAR-10과 Fashion-MNIST 에 대해서 실험했습니다. GEOM에서 사용된 72가지 transformation을 똑같이 사용했습니다. 이미지에 대한 random affine transformation은 성능이 좋게 나오지 않았는데, 이는 랜덤 transfomation이 인접 픽셀 간 공간 정보를 왜곡하고 이 왜곡된 정보를 CNN이 효과적으로 포착했기 때문에 오히려 성능이 더 낮게 나왔습니다.
밑의 실험 결과에서 볼 수 있듯이 GOAD가 다른 baseline 방법들에 비해 높은 성능을 보인 것을 알 수 있습니다. 실험은 다른 논문과 마찬가지로 one-vs-all 방법으로 진행되었습니다.

Adversarial robustness
Transformation이 알려진 알려진 네트워크와 랜덤 transformation이 사용된 네트워크에 대해서 adversarial example에 대한 classification error를 비교합니다. 결과 랜덤 transfomration이 사용된 네트워크의 classification 에러가 제일 덜 높아졌으며 이는 랜덤 transformation의 이점을 실험적으로 증명했다고 볼 수 있습니다.
Tabular data experiments
Tabular data 실험에는 사이버 침입 감지 데이터셋인 KDD와 UCI 레포에서 추출된 메디컬 데이터인 Arrhythmia와 Thyroid가 사용되었습니다. Tabular data에서는 정상 분포에서 추출한 랜덤 transformation이 사용되었으며, 데이터의 차원을 줄이도록 설계했습니다. ($W\in R^{L\times r}$, $L$은 데이터 차원, $r$은 축소된 차원) 모델로는 fully-connected와 (실제 구현에서는 kernel 사이즈가 1인 convolution) leaky-ReLU가 사용되었습니다. 실험 결과는 다음 표와 같고 GOAD가 다른 방법들에 비해 더 높은 성능을 보인 것을 확인할 수 있습니다.

또한, 랜덤 transformation의 개수 (the number of auxiliary tasks)가 많아질 수록 성능이 증가하면서 분산이 감소하는 것을 확인할 수 있습니다.

Contaminated data
논문이 비록 semi-supervised 시나리오를 가정했지만 anomaly로 일정 비율 오염되어 있을 때의 성능을 확인해봅니다. 다음 그림과 같이 baseline에 비하여 훈련 데이터에 anomaly가 섞여있더라도 더 좋은 성능을 나타냄을 확인할 수 있습니다.

Choosing the margin parameter s
Center triplet loss의 클래스 클러스터 간의 거리를 조절하는 마진 $s$에 대한 민감도는 딱히 크지 않습니다. 아래 그림에서 볼 수 있듯이 $s=0.1, s=1$의 성능이 거의 비슷한 것을 볼 수 있습니다. 논문에서는 $s=1$을 사용합니다.

참조
'Machine Learning Tasks > Anomaly Detection' 카테고리의 다른 글
| Local Outlier Factor (LOF) (0) | 2021.05.01 |
|---|---|
| RAPP (0) | 2021.04.30 |
| Deep Anomaly Detection Using Geometric Transformations (2) | 2021.03.16 |
| Deep Semi-Supervised Anomaly Detection (1) | 2021.03.14 |
| Deep One-Class Classification (0) | 2021.03.14 |



