우리가 모델링할 수 있는 불확실성, uncertainty는 크게 두 가지 종류가 있습니다. 첫 번째는 데이터 자체에 담겨 있는 고유 노이즈로 인한 aleatoric uncentainty이고 두 번째는 모델이 데이터를 충분히 설명하지 못하는 epistemic uncertainty입니다.
딥러닝 모델이 강력한 성능으로 여러 분야에서 다양하게 활용되고 있지만 오히려 그 강력한 성능으로 인해 결과가 무작정 신뢰되는 오류를 초래합니다. 최근에 일어난 자율주행 자동차의 판단 오류로 인한 사망사고나 흑인을 고릴라로 잘못 판단한 사고 등 딥러닝 모델 결과에 대한 신뢰성을 확보하는 요구는 점차 커지고 있습니다.
이번 포스트는 NIPS 2017에 발표된 Bayesian Neural Networks 분야의 거두 Yarin Gal의 'What Uncertainty Do We Need in Bayesian Deep Learning for Computer Vision?' 이란 논문을 살펴보려 합니다. 이 논문은 컴퓨터 비젼의 대표 분야인 semantic segmentation과 depth regression task에서 aleatoric/epistemic uncertainty를 통함한 framework를 제시하였습니다.
Uncertainty
먼저 각 uncertainty 종류에 대해 살펴보겠습니다. Aleatoric uncertainty는 데이터에 포함된 고유 노이즈로 발생하는 불확실성 입니다. 우리가 센서 등으로 데이터를 취득할 때 그 데이터가 깨끗하다고 무조건 단정지을 수 없듯이 측정 단계부터 포함된 데이터 고유 노이즈로 인한 것으로서 데이터를 많이 취득한다고 해서 없어지지 않습니다. Aleatoric uncertainty는 입력 데이터의 종류마다 노이즈가 일정하다고 가정한 homoscedastic uncertainty와 입력마다 노이즈가 서로 다른 heteroscedastic uncertainty로 나눌 수 있습니다. Practical한 상황에서는 당연히 heteroscedastic uncertainty를 모델링 하는 것이 더 중요하겠죠.
반면 epistemic uncertainty는 모델 파라미터의 uncertainty입니다. 즉, 우리의 모델이 결과를 얼마나 확신할 수 있느냐의 측정이죠. 따라서 epistemic uncertainty는 데이터가 충분할수록 줄일 수 있습니다.
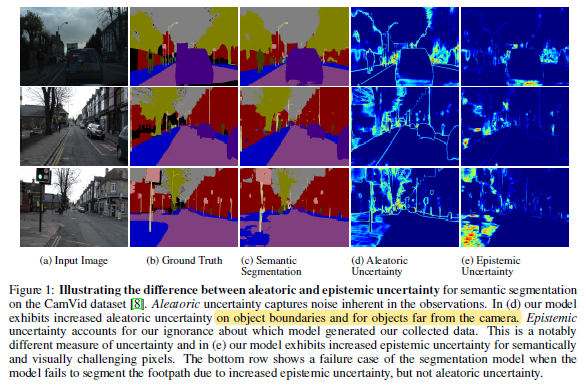
위의 (d)와 (e)는 각각 aleatoric, epistemic uncertainty를 표현한 것으로서 (d)에서는 보통 물체의 경계와 같은 사진 육안상으로도 애매한 부분에서 highlight가 된 것을 볼 수 있고 (e)에서는 모델 자체가 segmentation을 잘 수행하지 못한, 모델 결과의 신뢰도가 낮은 부분이 highlight가 되어 있습니다.
이러한 각 uncertainty의 특성에 따라 Yarin Gal은 aleotoric uncertainty와 epistemic uncertainty를 합쳐 모델링하는 방법을 제안합니다. Epistemic uncertainty는 데이터가 많아질수록 줄일 수 있으면서 이상 데이터도 파악할 수 있으며, 데이터가 많아도 항상 발생하는 aleatoric uncertainty 또한 모델링 함으로써 데이터 고유의 노이즈로 인한 불확실성도 함께 포착하자는 것이죠.
Bayesian deep learning을 이용한 uncertainty 모델링은 주로 aleatoric, epistemic uncertainty를 개별적으로 모델링해 왔습니다. Epistemic uncertainty의 경우 모델의 불확실성으로 모델의 파라미터에 대한 확률 분포를 모델링하여 측정되며 aleatoric uncertainty의 경우 모델의 출력단에 확률 분포를 모델링하여 이루어집니다.
Epistemic uncertainty in Bayesian Deep Learning
Epistemic uncertainty를 모델링하기 위해 모델 파라미터에 prior distribution $W \sim N(0,I)$를 가정하여 bayesian neural networks의 형태로 표현합니다. Bayesian neural networks의 파라미터는 결정론적으로 정해지는 일반적인 neural networks의 파라미터와 다르게 데이터셋 $X={x_1, ..., x_N}$, $Y={y_1,...,y_N}$이 주어졌을 때의 파라미터에 대한 posterior distribution인 $p(W|X,Y)$를 통해 확률 분포로서 존재합니다. 따라서 inference 시에 $p(W|X, Y)$, 데이터로부터 그럴듯한 $W$를 샘플링하게 됩니다.
Regression task의 경우 bayesian neural networks의 likelihood는 다음과 같이 $p(y|f^W(x)) = N(f^W (x), \sigma^2)$로 정의할 수 있습니다. Classification 경우에는 softmax를 통해 likelihood를 정의합니다 ($p(y|f^W(x))=Softmax(f^W(x))$ ).
하지만 posterior distribution은 $p(W|X,Y)$=$p(Y|X,W)p(W) / p(Y|X)$ 이므로 해석적으로 구할 수 없습니다. 따라서 variational inference와 같이 $p(W|X,Y)$를 잘 근사하는 $q_\theta^{*}(W)$를 정의하여 사용하게 됩니다. 즉, $W$가 확률 분포로 되어 있어 가능한 $W$에 따른 모든 결과가 필요한데 이를 직접적으로 구할 수 없으므로 간단한 분포인 $q_\theta^{*}(W)$를 정의하여 $q$를 정의하는 $\theta$를 구하는 문제로 바꾸는 것이죠.
Bayesian neural networks에서는 이를 dropout을 이용하여 구현합니다. Dropout은 각 파라미터 당 binomial distribution 확률 분포를 적용하는 것이니, 두 개의 Gaussian distribution의 조합인 $q_\theta^{*}(W)$로부터 샘플링한 $\hat{W}$로부터 inference하는 것과 dropout을 적용하는 것이 같다는 것이죠. (내용이 어렵지만 결론은 training/test phase에서 dropout을 사용하는 것이 $W$에 대한 variational inference 하는 것과 같다는 말입니다)
결론적으로 dropout variational inference를 위한 목적함수는 Equation 1과 같고 regression의 경우 negative log likelihood는 Gaussian likelihood로 Equation 2와 같이 표현할 수 있습니다. Equation 2의 $\sigma$는 입력의 노이즈를 포착하는 파리미터입니다. 두 Equation의 $\hat{W}$는 $q_{\theta}^{*} (W)$로부터 샘플링된 값으로 $\theta$는 dropout 경우에 neural network 파라미터가 됩니다.
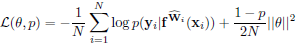
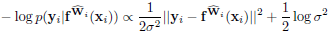
Epistemic uncertainty는 많은 데이터를 사용하면 줄일 수 있으며, 모델 파라미터를 확률 분포로 모델링하기 때문에 자연스럽게 prediction uncertainty를 유도합니다. Classification의 경우 Equation 3과 같이 Monte Carlo 방법으로 $T$번 샘플링한 $\hat{W}$에 대한 평균으로 확률을 구할 수 있으며, entropy $H(p)$를 통해 uncertainty를 표현할 수 있습니다.

Regression에 대해서는 Equation 4와 같은 predictive variance를 통해 epistemic uncertainty를 표현합니다. Equation 4의 $E(y)$ $\approx$ $\frac{1}{T}\sum f^{\hat{W}_t} (x)$ 를 통해 예측치의 분산을 구하며 첫 번째 $\sigma$는 뒤의 aleatoric uncertainty에서 다룰 데이터의 노이즈로 인한 variance입니다.
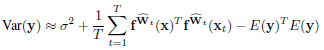
Heteroscedastic aleatoric uncertainty
Aleatoric uncertainty를 포착하기 위해서는 데이터의 노이즈로 인한 $\sigma$를 조절해야 합니다. Homoscedastic 같은 경우에는 모든 입력에 대해 노이즈가 동일하다고 가정하나 일반적으로 입력 각각에 따라 노이즈 레벨이 다른 heteroscedastic 경우를 고려합니다. 따라서 data-dependent하게 Equation 5와 같이 쓸 수 있습니다.
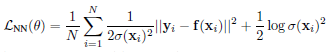
Equation 5를 보면 $\sigma$는 데이터에 따라 다른 값을 가지고 있으며 모델의 출력 $f(x)$는 고정되어 있습니다. 추후에 살펴보겠지만 aleatoric uncertainty를 고려할 때는 dropout을 사용하지 않으며, 이는 모델의 파라미터를 하나의 값으로 고정시켜 point 추정을 하는 MAP inference라 할 수 있습니다.
'Machine Learning Tasks > ETC' 카테고리의 다른 글
| 불확실성, Aleatoric and Epistemic Uncertainty (2) (0) | 2021.03.27 |
|---|
