이번 포스트에서는 너비우선탐색 (BFS, Breadth First Search) 를 살펴보겠습니다. 스택이나 재귀로 구현하는 깊이우선탐색과 달리 너비우선탐색은 First-In First-Out (FIFO) 의 큐 자료구조를 사용해 구현하며, 다익스트라 알고리즘과 같은 최단 경로를 구하는 데 사용됩니다.
코드를 어떻게 구현하게 될까요? 선입선출의 큐를 이용하니 파이썬의 list나 collections 모듈의 deque를 이용할 수 있을 것 같습니다. 깊이우선탐색에서의 스택과 달리 큐는 배열의 첫 번째 원소가 추출되는 구조이니 해당 정점의 인접점들을 모두 방문하고 다음 레벨의 정점을 방문하게 됩니다.
깊이우선탐색과 같은 그래프 예로 코드를 한 번 살펴보겠습니다.
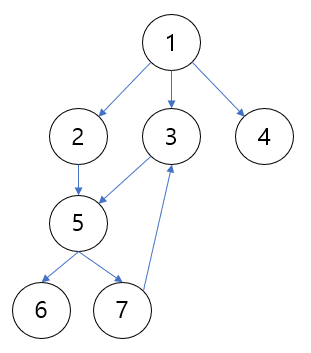
graph = {1: [2,3,4], 2: [5], 3: [5], 4: [], 5: [6,7], 6: [], 7: [3] }
파이썬 코드
from collections import deque
def bfs(start_v): # 시작점 (start_v) 부터 시작
## Queue 선언
queue = deque([start_v])
## 그래프 탐색 결과
result = [start_v]
while queue: # queue에 원소가 남아있을 때까지
vertex = queue.popleft() # List라면 pop(0)
for neighbor_vertex in graph[vertex]:
## 인접점이 결과에 없을 경우 결과와 queue에 추가
if neighbor_vertex not in result:
queue.append(neighbor_vetex)
result.append(neighbor_vertex)
return result
순회 결과는 어떻게 될까요? 1부터 시작했을 때 queue와 result에 2,3,4가 담기고 2가 다음 vertex로 추출됩니다. 2에 대한 인접점 5는 queue와 result에 추가되지만 깊이우선탐색 때의 스택과 달리 큐이므로 리스트의 처음 인덱스가 추출되므로 3이 다음 vertex로 추출됩니다. 최종 결과는 다음과 같습니다.
print(bfs(1))
=> [1,2,3,4,5,6,7]깊이우선탐색 때와 달리 같은 레벨의 인접점부터 순회하고 그 다음 레벨의 인접점을 순회하는 것을 알 수 있습니다. 이를 구현하기 위해 큐를 사용해서 구현한 것입니다.
참고로, deque 대신 일반 리스트를 쓸 때에는 deque의 popleft() 메소드 대신 리스트의 pop(0)을 사용하여야 합니다. deque 자료구조를 사용한 이유는 deque의 popleft()는 $O(1)$의 상수시간이 소요되지만 리스트의 pop(0)은 복사로 인해 $O(n)$의 시간 복잡도가 소요되기 때문입니다.
홍머스 정리
- BFS는 같은 레벨의 인접점부터 순회하므로 큐로 구현
- 재귀로는 구현 불가
참조
- <파이썬 알고리즘 인터뷰>, p326-327
'Theory > Algorithms' 카테고리의 다른 글
| 다이나믹 프로그래밍 (Dynamic Programming) (0) | 2021.02.23 |
|---|---|
| 이진 탐색 (binary search) (0) | 2021.02.23 |
| 그래프 (1) - 깊이우선탐색 (DFS, Depth First Search) (0) | 2021.02.22 |
| 안정 정렬 vs 불안정 정렬 (0) | 2021.02.22 |
| 병합 정렬 / 합병 정렬 (Merge Sort) (0) | 2021.02.22 |

