다이나믹 프로그래밍 (Dynamic Programming) 은 리차드 벨만 (Richard Bellman) 이 1953년에 고안한 알고리즘입니다. 우리 말로 "동적 계획법" 이지만 동적이라 함은 보통 프로그래밍에서 프로그램이 실행되는 도중에 필요한 메모리를 그때마다 할당하는 기법을 뜻하고 다이나믹 프로그래밍에서는 딱히 큰 의미는 없습니다.
다이나믹 프로그래밍은 문제를 각각의 작은 문제로 나누어 해결한 결과를 저장해두었다가 나중의 큰 문제의 결과와 합하여 풀이하는 방식입니다. 그럼 어느 경우에 다이나믹 프로그래밍을 주로 사용할까요?
- 문제가 최적 부분 구조 (Optimal Substructure) 를 가지고,
- 동일한 작은 문제를 반복적으로 해결해야 하는 경우 (중복되는 부분 문제) 에 적합합니다.
문제가 최적 부분 구조를 가지고 있다는 것은 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 최적 해결로 큰 문제를 해결할 수 있다는 것입니다. 또한, 중복된 하위 문제들의 결과를 저장해 두었다가 큰 문제의 풀이에 사용합니다.
다이나믹 프로그래밍의 방법론은 다음과 같은 2가지 방향으로 나누어집니다.
- 상향식 (타뷸레이션)
더 작은 하위 문제부터 살펴본 다음, 하위 문제의 정답을 이용해 더 큰 문제의 정답을 풀어나갑니다. 타뷸레이션이라 불리는 이유는 작은 문제부터 큰 문제까지 하나하나 테이블을 채워나간다는 의미입니다. 일반적인 다이나믹 프로그래밍이란 보통 이 상향식 방법을 말합니다. - 하향식 (메모이제이션)
이 방식은 큰 문제에서 하위 문제로 접근해서 하위 문제에 대한 정답을 계산했는지 확인해가며 문제를 푸는 방식입니다. 메모이제이션이란 말처럼 하위 문제의 정답을 메모하면서 그 문제를 호출하면 메모했던 결과를 가져옵니다. 캐쉬와 비슷하다고 생각할 수 있습니다.
다이나믹 프로그래밍의 대표적인 예시인 피보나치 수열로 살펴보겠습니다.
피보나치 수열 (fibonacci sequence)
피보나치 수열은 $a_n = a_{n-1}+a_{n-2}, a_1=a_2=1, n\geqslant 2$ 의 점화식을 가지는 수열로 13세기 이탈리아의 수학자 레오나르도 피보나치 (Leonardo Fibonacci) 가 토끼의 번식을 가지고 추정한 문제입니다 (인덱스는 1부터 시작한다고 가정합니다). 다이나믹 프로그래밍을 살펴보기 전 피보나치 수열은 단순한 재귀 함수로 풀 수 있습니다.
재귀 풀이
def fibonacci(n):
if n <= 2:
return 1
return fibonacci(n-1) + fibonacci(n-2)위의 점화식을 그대로 구현했습니다. 이렇게 해도 문제는 풀리지만 다음과 같은 문제가 있습니다.
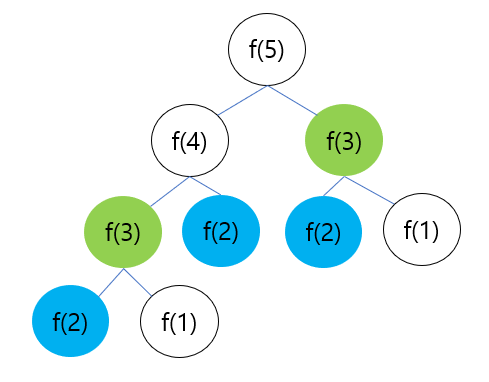
다섯 번째 피보나치 수를 구하고 싶을 때, 위 점화식을 하위 문제로 쪼갤 수 있고, f(2)나 f(3)은 중복되는 부분 문제로서 여러 번 호출됩니다. 중복되는 하위 문제가 여러 번 호출되니 시간 복잡도 측면에서 좋지 않겠죠?
다이나믹 프로그래밍의 핵심은 중복된 하위 문제의 결과를 저장해뒀다가 추후 큰 문제 풀이에 사용한다는 점입니다. 따라서, 해당 하위 문제는 한 번만 계산하게 됩니다. 그림으로 보면 다음과 같습니다. 재귀 풀이시 여러 번 호출된 f(2), f(3)의 결과가 어딘가 미리 저장되어 있다면 그 값만 불러오면 되므로 다시 계산할 필요가 없습니다.
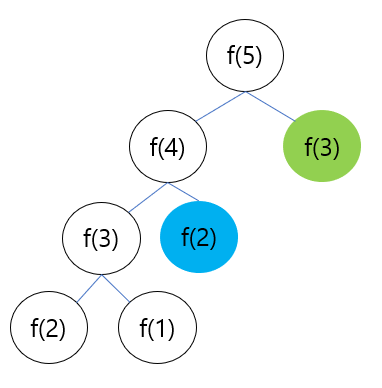
하향식 (메모이제이션) 풀이
from collections import defaultdict
dp = defaultdict(int)
def fibonacci(n):
if n <= 2:
return 1
## 메모가 있으면 그 값을 return
if dp[n]:
return dp[n]
## 메모가 없으면 점화식으로부터 계산하여 메모
dp[n] = fibonacci(n-1) + fibonacci(n-2)
return dp[n]하향식, 탑-다운이므로 n부터 시작해 각 값마다 메모가 있는지 계산합니다. 메모가 있다면 그 값을 return합니다.
상향식 (테뷸레이션) 풀이
from collections import defaultdict
dp = defaultdict(int)
def fibonacci(n):
## 초기값
dp[1] = dp[2] = 1
for i in range(3, n+1):
## 점화식으로 dp 테이블 채움
dp[i] = dp[i-1] + dp[i-2]
return dp[n]상향식, 보텀-업이므로 초기값부터 채운 후 점화식에 따라 값을 채워갑니다. 이 때, dp 테이블인 dp값을 작은 문제부터 하나하나 채워나간다는 의미에서 테뷸레이션이라 볼 수 있습니다.
시간 복잡도
피보나치 수열의 재귀 풀이는 중복되 하위 문제를 여러 번 계산하기 때문에 $O(2^n)$의 시간 복잡도가 소요됩니다. 하지만 다이나믹 프로그래밍의 경우 문제에 대한 값을 계산했을 때 따로 저장해두고 사용하므로 $O(n)$의 시간 복잡도가 소요됩니다.
분할 정복과의 관계
다이나믹 프로그래밍 또한 문제를 작은 문제로 분할하여 푼다는 점에서 분할 정복 알고리즘에 속합니다. 즉, 모두 최적 부분 구조를 가지고 있습니다. 하지만, 중복된 하위 문제를 가지고 있다는 점에서 퀵 정렬이나 그리디 알고리즘 같은 다른 분할 정복 알고리즘과는 차이가 있습니다. 예를 들어 퀵 정렬에서는 피벗을 통해 파티션을 나누는 하위 문제는 다시 호출되지 않습니다.
홍머스 정리
- 최적 부분 구조 (Optimal Substructure) + 중복된 하위 문제 (Overlapping Subproblems)
- 상향식 (tabulation), 하향식 (memoization), 문제마다 접근 방법이 다르다.
- 주어진 문제가 다이나믹 프로그래밍 문제인제 파악하는 것이 중요!
참조
- <파이썬 알고리즘 인터뷰>, p621-630
- www.youtube.com/watch?v=rWbjQphRE9A&list=PLVsNizTWUw7H9_of5YCB0FmsSc-K44y81&index=28
'Theory > Algorithms' 카테고리의 다른 글
| 자료구조 - 힙 (Heap) (0) | 2021.02.24 |
|---|---|
| 자료구조 - 스택 (Stack), 큐 (Queue) (0) | 2021.02.24 |
| 이진 탐색 (binary search) (0) | 2021.02.23 |
| 그래프 (2) - 너비우선탐색 (BFS, Breadth First Search) (0) | 2021.02.22 |
| 그래프 (1) - 깊이우선탐색 (DFS, Depth First Search) (0) | 2021.02.22 |

