힙은 부모가 항상 자식보다 작거나 같다 (최소힙)라는 특성을 만족하는 트리 기반의 자료구조입니다. 이번 포스트에서 다룰 힙은 최소힙이고 최소힙은 부모가 항상 자식보다 작기 때문에 트리의 루트가 가장 작은 값을 갖게 됩니다. 반대로 최대힙은 부모가 항상 자식보다 큰 트리가 되겠죠.
힙이라는 자료구조는 J.W.J. 윌리엄스가 1964년 힙 정렬 알고르짐을 고안하면서 파생된 부산물입니다. 보통 배열로 구현하며 다음 그림과 같이 부모와 자식 간의 상하 관계가 정의되어 있고 같은 레벨의 자식들끼리의 좌우 관계는 정의되어 있지 않습니다.
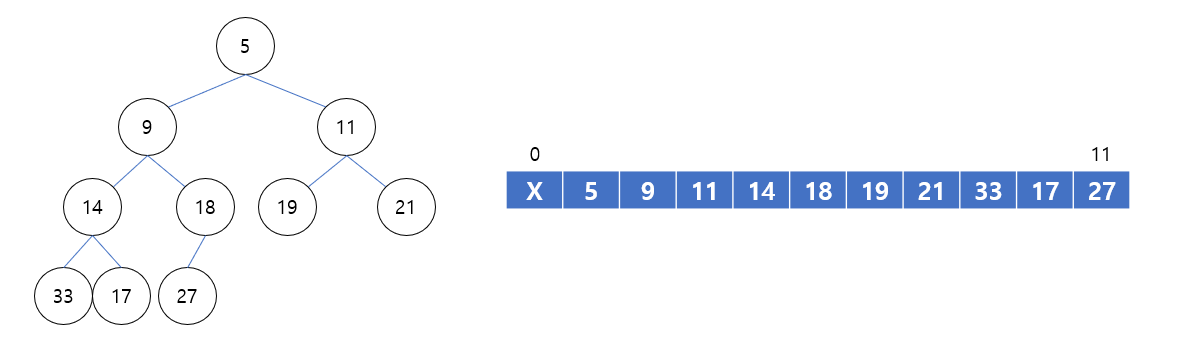
힙은 주로 배열로 구현되며, 위 그림 오른쪽처럼 배열로 표현할 수 있습니다. 루트 노드의 인덱스는 1부터 시작하고 그 다음 레벨 노드의 인덱스는 2,3, 그 다음 레벨 노드의 인덱스는 4,5,6,7 순으로 배열에 표현됩니다. 이처럼 노드 순서가 밑의 왼쪽부터 순서대로 차게 되는 트리를 거의 완전 트리 (Almost Complete Tree)라 하고 위 그림과 같이 자식이 둘인 트리는 이진 트리 (Binary Tree)라 합니다. 여기서는 이진힙 (Binary Heap)이 되겠네요.
언급했듯이 부모는 자식보다 항상 작게 되어 있지만 왼쪽 밑 노드 33, 17을 보면 좌우 관계는 정의되어 있지 않습니다. 이것이 추후 살펴볼 이진탐색트리 (Binary Search Tree)와의 결정적인 차이점입니다.
파이썬 구현
먼저 힙을 배열로 구현했을 때, 어떠한 연산이 필요할까요?
삽입
-
힙에 요소를 추가하기 위해서는 거의 완전 트리 조건을 만족시키기 위해 가장 하위레벨의 최대한 왼쪽으로 삽입합니다. 배열의 가장 마지막에 append 하는 것과 같습니다.
-
이제 부모가 자식 값보다 작도록 정렬을 해야합니다. 삽입된 위치의 부모의 값과 비교해 부모 값이 더 큰 경우 swap합니다.
-
2번 과정을 반복해서 올바른 위치를 찾습니다. 이 때, 삽입된 원소가 가장 작을 경우 힙의 루트까지 올라가게 되겠죠.
추출
-
추출은 무조건 루트를 추출합니다.
-
삽입 때와 마찬가지로 힙을 재정렬해야합니다. 가장 하위레벨의 가장 오른쪽에 있는 원소 (배열의 마지막 원소)를 루트에 삽입합니다.
-
루트의 원소와 자식들과 비교하면서 자식의 값이 더 작은 경우 swap합니다. 이 과정을 올바른 위치를 찾을 때까지 반복합니다.
삽입과 추출 모두 배열의 원소를 재정렬하는 과정을 포함하게 됩니다. 이 때, 상위 레벨 노드와의 값만을 비교하므로 힙의 크기 (배열의 길이)가 $n$일 경우, $O(\log n)$의 시간 복잡도가 소요됩니다.
파이썬 코드는 다음과 같습니다. 참고로 힙은 인덱스를 1부터 사용합니다.
class BinaryHeap(object):
def __init__(self):
self.items = [None] # 배열의 맨 처음 인덱스 (0)은 사용하지 않음
def __len__(self):
return len(self.items) - 1 # 맨 처음 원소를 빼고 return
## 삽입 후 힙 재정렬하는 함수
def _up_heap(self):
## 부모 노드 인덱스 추출
parent_index = len(self) // 2
while parent_index > 0:
## 부모 노드가 더 클 경우
if self.items[i] < self.items[parent_index]:
## 부모 노드와 swap
self.items[i], self.items[parent_index] = \
self.items[parent_index], self.items[i]
## 부모 노드로 노드 인덱스 변환
i = parent
## 부모 노드는 기존 노드의 절반
parent = i // 2
## 삽입 함수
def insertion(self, item):
## 가장 하위레벨의 최대한 왼쪽 (배열 마지막)에 원소 추가
self.items.append(item)
self._up_heap() # 힙 재정렬
## 추출 후 힙 재정렬하는 함수
def _down_heap(self, idx):
left = idx * 2 # 왼쪽 자식 노드 인덱스
right = idx * 2 + 1 # 오른쪽 자식 노드 인덱스
smallest = idx
## 왼쪽 노드 값보다 클 경우 swap
if left <= len(self) and self.items[left] < self.items[smallest]:
smallest = left
## 오른쪽 노드 값보다 클 경우 swap
elif right <= len(self) and self.items[right] < self.items[smallest]:
smallest = right
## 인덱스가 바뀌었을 경우 swap하고 재귀적으로 호출
if smallest != idx:
self.items[idx], self.items[smallest] = \
self.items[smallest], self.items[idx]
self._down_heap(smallest)
## 추출 함수
def extract(self):
extracted = self.items[1] # 루트 노드 추출
self.items[1] = self.items.pop() # 마지막 원소 루트로 대입하고 삭제
self._down_heap(1)
return extracted
파이썬에서의 힙
파이썬에서는 heapq라는 최소힙을 구현한 내장 모듈이 있습니다. heapq 모듈의 heappush() 메소드는 삽입, heappop() 메소드는 추출에 대응됩니다. 주어진 어떤 리스트를 heapify에서 힙으로 만들 수도 있습니다. 파이썬에서는 일반 리스트를 이용해 heapify나 heappush를 이용해 쉽게 힙 연산을 구현할 수 있습니다.
heappush(heap, item)

heapify(x)

- heapify 메소드는 in-place 메소드로 리스트를 힙으로 바꾼 결과물을 다른 변수에 할당할 필요가 없습니다.
홍머스 정리
- 힙은 거의 완전 트리 기반의 자료구조로 최소힙은 부모 노드는 자식 노드보다 항상 작거나 같다.
- 파이썬에서는 heapq (heapify, heappush, heappop)
- 일반적으로 이진힙 사용
참조
- <파이썬 알고리즘 인터뷰>, p447-455
- docs.python.org/3/library/heapq.html
'Theory > Algorithms' 카테고리의 다른 글
| 최단 경로 문제 (1) - 다익스트라 알고리즘 (0) | 2021.03.01 |
|---|---|
| 자료구조 - 해시 테이블 (Hash Table) (0) | 2021.02.25 |
| 자료구조 - 스택 (Stack), 큐 (Queue) (0) | 2021.02.24 |
| 다이나믹 프로그래밍 (Dynamic Programming) (0) | 2021.02.23 |
| 이진 탐색 (binary search) (0) | 2021.02.23 |


