해시 테이블은 임의 크기 데이터를 고정 크기 값으로 매핑하는 해시 함수를 기반으로 동작하는 대부분의 연산의 시간 복잡도가 상수 시간 $O(1)$ 이 소요되는 자료구조입니다. 한스 피터 룬 (Hans Peter Luhn)이 처음 사용한 것으로 알려져 있으며, 현대에도 각종 프로그래밍 및 알고리즘에 중요하게 사용되는 자료구조입니다.
해시 테이블은 키:값 (key:value) 의 형태로 데이터를 저장합니다. 키 (key) 값에는 해시 함수를 적용해 값이 저장된 배열 (버킷)에 대한 고유한 인덱스를 생성하고 이 인덱스를 활용해 값을 저장하거나 검색합니다. 따라서 키에 대해 해시 함수를 한 번만 적용하면 되니, 저장이나 검색에 $O(1)$의 상수 시간 복잡도가 소요됩니다.

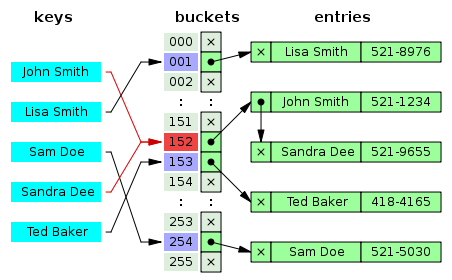
위 그림에서 키인 'John Smith', 'Lisa Smith', 'Sandra Dee'는 해시 함수에 의해 특정 인덱스로 매핑됩니다. 이렇게 해시 함수를 이용해서 해당 키 값에 대한 인덱스를 구하는 것을 해싱 (Hashing)이라고 합니다. 그렇다면 해시 함수에는 어떤 함수가 사용될까요?
- Modulo-Division method: 입력값 ($h(key)$)을 테이블의 크기로 나누어 나머지 값을 인덱스로 사용하는 방법입니다. 가장 간단합니다. 이미 많은 키 세트가 충분히 랜덤하고 테이블의 크기가 충분히 크다면 잘 동작합니다. $h(key)$는 수학적으로 소수의 거듭제곱 연산으로 구합니다.
- Digit folding: 키의 ASCII 코드에 대해 이 값을 합한 데이터를 테이블의 인덱스로 사용합니다.
- Universal Hashing: 다수의 해시 함수를 함수 공간에 넣어두고 무작위로 해시 함수를 선택해 테이블의 인덱스로 만듭니다.
최상의 해시 함수의 조건은 무엇일까요? 서로 다른 키 값에 대해 각각 다른 해싱 값을 테이블에 잘 분산해주는 것이겠죠. 하지만, 테이블의 크기가 한정되 있는 이상 서로 다른 키가 같은 해싱 값에 매핑되는 해시 충돌 (Hash Collision)은 일어날 수밖에 없습니다.
해시 충돌
충돌은 얼마나 자주 일어날까요? 생일 문제를 생각해보면 23명만 모여도 같은 생일이 존재할 확률은 50%가 넘고 57명이 모이면 99%를 넘어선다고 합니다. 그렇다면 해시 테이블에서는 충돌을 어떻게 관리할까요?
개별 체이닝 (Separate Chaining)
가장 기본적인 방식입니다. 충돌 시 추가 메모리를 사용하여 연결 리스트로 연결하는 방식으로 테이블의 확장이 필요없고 간단하게 구현이 가능합니다. 하지만 데이터가 많아질 수록 체이닝된 데이터가 많아지고, 최악의 경우 모든 키에 대해 해시충돌이 발생했을 때 시간 복잡도가 $O(n)$이 되버립니다. 입니다. 실제로 Java8의 해시 테이블은 개별 체이닝을 채택하고 있는데 연결 리스트 구조를 자가 균형 이진 탐색 트리로 개선하는 형태로 사용합니다.
오픈 어드레싱 (Open Addressing)
오픈 어드레싱은 충돌 발생 시 해당 인덱스에 연결을 하는 것이 아니라 탐사를 통해 빈 공간을 찾아나서는 방법입니다. 따라서, 사실상 무한히 데이터를 저장할 수 있는 개별 체이닝과는 달리 해시 테이블 크기 이상은 저장할 수 없고 모든 키가 자신의 해싱 값과 일치하는 주소에 저장된다는 보장이 없습니다.
오픈 어드레싱은 충돌이 발생할 경우 탐색 (probing)을 하게 되는데, 현재의 해싱 인덱스로부터 고정폭만큼 이동하여 비어있는 버킷에 저장하는 Linear Probing 방식과 고정폭이 대신 폭을 제곱만큼 늘리는 (처음 충돌은 1칸, 두 번째 충돌은 4칸, 세 번째 충돌은 9칸...) Quadratic Probing 방식이 있습니다.

이 중 선형 탐사 방법은 구현도 간단하고 성능이 좋은 편이지만 해시 테이블에 저장되는 데이터들이 고르게 분포하지 않고 뭉치는 클러스터링 (Clustering) 되는 현상이 일어나게 됩니다. 즉, 테이블 여기 저기에 연속된 데이터 그룹이 생기게 되고 특정 인덱스 근처에 뭉치게 되는 것이죠. 따라서 탐사 시간이 오래 걸리게 될 뿐 아니라 해싱 효율이 떨어지게 되는 원인이 되기도 합니다.
오픈 어드레싱 방식은 테이블의 크기보다 데이터 양이 더 큰 경우 더 삽입할 수 없으므로 일정 이상 (로드 팩터) 채워지면 더 큰 크기의 버킷을 생성한 후 여기에 기존의 테이블을 복사하는 리해싱 (Rehashing) 작업을 거치게 됩니다.
로드 팩터 (Load Factor)
로드 팩터란 해시 테이블에 저장된 개수 $n$을 버킷의 크기 $k$로 나눈 $n/k$ 값으로 이 비율에 따라서 해시 테이블의 크기를 조정할지를 결정합니다. 로드 팩터가 증가할 수록 해싱 테이블의 효율과 성능이 떨어지게 되므로 자바의 경우 로드 팩터가 0.75, 파이썬은 0.66 이상일 경우 해시 테이블의 공간을 재할당합니다.
파이썬에서의 해시 테이블
파이썬에서의 해시 테이블은 당연히 딕셔너리 (dict()) 입니다. 파이썬에서는 자바와는 달리 오픈 어드레싱을 채택하고 있습니다. 이는 체이닝을 사용하게 되면 연결리스트를 만들기 위해 추가 메모리가 필요하고 추가 메모리 할당은 상대적으로 느린 작업이기 때문에 오버헤드가 높아지기 때문이라고 합니다.
파이썬의 딕셔너리는 문자, 숫자, 집합, 튜플 등의 불변 객체를 모두 키로 사용 가능하며 입력과 조회 모두 $O(1)$에 가능합니다. 참고로 파이썬 3.6까지는 딕셔너리의 입력 순서가 유지되지 않았습니다. 파이썬 3.7부터는 내부적으로 인덱스를 이용해서 입력 순서를 유지하도록 개선되었습니다. 코딩 테스트에서는 구현 환경이 각각 다를 수가 있으므로 딕셔너리의 순서 유지가 필요할 경우 dict() 보다는 collections 모듈의 OrderedDict() 를 사용하는 것이 낫습니다.
홍머스 정리
- 해시 테이블, 해시 함수, 딕셔너리
- 파이썬은 오픈 어드레싱 방법
- 시간 복잡도 $O(1)$
참조
- <파이썬 알고리즘 인터뷰>, p279-290
- mangkyu.tistory.com/102
'Theory > Algorithms' 카테고리의 다른 글
| 최단 경로 문제 (2) - 플로이드 워셜 알고리즘 (0) | 2021.03.01 |
|---|---|
| 최단 경로 문제 (1) - 다익스트라 알고리즘 (0) | 2021.03.01 |
| 자료구조 - 힙 (Heap) (0) | 2021.02.24 |
| 자료구조 - 스택 (Stack), 큐 (Queue) (0) | 2021.02.24 |
| 다이나믹 프로그래밍 (Dynamic Programming) (0) | 2021.02.23 |


