지난 포스트에서 수행한 선형 회귀는 독립 변수들의 선형 결합으로 종속 변수를 표현하기 때문에 변수들이 선형으로 분포하지 않거나 구간 별로 기울기가 다르게 적용되는 경우 설명에 한계가 있습니다. 이를 해결하기 위한 가장 간단한 방법으로는 각 독립 변수에 대한 고차원의 다항식을 적용하여 비선형적으로 종속 변수를 표현하는 방법이 있습니다.
Examples
Simple example
간단한 numpy array를 선언하여 종속 변수에 대해 독립 변수를 다항식으로 구성하여 설명해 보겠습니다. 독립 변수의 다항식화는 sklearn.preprocessing 모듈의 PolynomialFeatures 함수를 사용해 쉽게 구현할 수 있으며 2차원의 데이터 [a,b]를 가지고 있을 때 디폴트로 [1,a,b,a^2,ab,b^2]의 feature를 생성합니다.
| Parameters | Default | Description |
| degree | 2 | 다항식의 차수 |
| interaction_only | False | True일 경우 feature 간의 상호작용만 반영하고 power 항은 생성하지 않음. |
| include_bias | True | False 일 경우 bias 항 (1) 을 생성하지 않음 |
import numpy as np
X = np.array([258.0, 270.0, 294.0,
320.0, 342.0, 368.0,
396.0, 446.0, 480.0, 586.0])[:, np.newaxis]
y = np.array([236.4, 234.4, 252.8,
298.6, 314.2, 342.2,
360.8, 368.0, 391.2,
390.8])
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
lr = LinearRegression()
pr = LinearRegression()
quadratic = PolynomialFeatures(degree=2)
X_quad = quadratic.fit_transform(X)
# 선형 특성 학습
lr.fit(X, y)
X_fit = np.arange(250, 600, 10)[:, np.newaxis]
y_lin_fit = lr.predict(X_fit)
# 이차항 특성 학습
pr.fit(X_quad, y)
y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))
import matplotlib.pyplot as plt
# 결과 그래프
plt.scatter(X, y, label='training points')
plt.plot(X_fit, y_lin_fit, label='linear fit', linestyle='--')
plt.plot(X_fit, y_quad_fit, label='quadratic fit')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()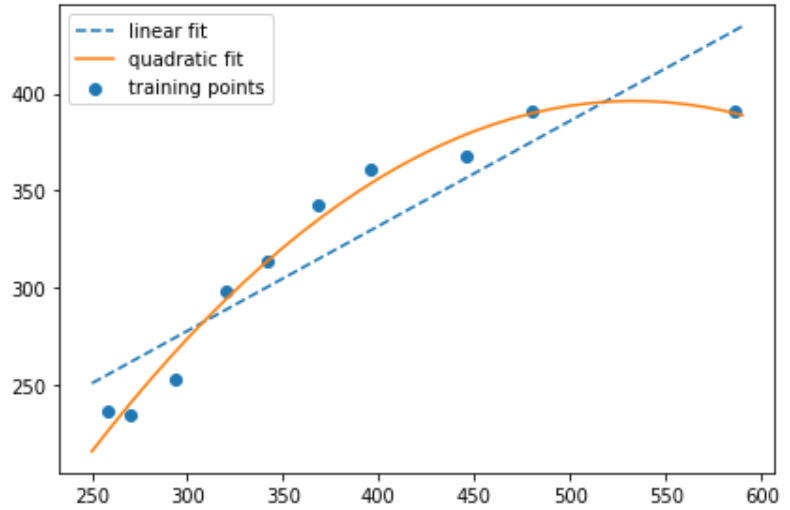
다항식을 이용한 단순 회귀
지난 포스트의 집값 데이터를 이용해 하나의 독립 변수를 2차항으로 만들어 단순 회귀를 수행해 보겠습니다. PolynomialFeature 의 include_bias 파라미터를 False로 지정했으므로 본래 feature와 제곱한 feature가 생성된 것을 확인할 수 있습니다.
import pandas as pd
df = pd.read_csv('/content/drive/MyDrive/Posco/Regression/Data/housing_data.txt', sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
#회귀분석을 수행할 데이터 추출
X = df[['LSTAT']].values
y = df['MEDV'].values
#훈련 데이터와 테스트 데이터를 7:3으로 분할
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
from sklearn.preprocessing import PolynomialFeatures #다항식 변환
# 다항식 변환
poly = PolynomialFeatures(degree=2, include_bias=False)
#데이터 변환
X_train_poly=poly.fit_transform(X_train)
X_test_poly=poly.fit_transform(X_test)
print('원래 데이터: ', X_train.shape)
print('2차항 변환 데이터: ', X_train_poly.shape)
print('원래 데이터: ', X_test.shape)
print('2차항 변환 데이터: ', X_test_poly.shape) 
이후 모델을 fitting 시키고 mean squared error와 $R^2$ 결과를 비교해보면,
'''일차 선형'''
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
print('일차 선형')
print('훈련 MSE: %.3f, 테스트 MSE: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('훈련 R^2: %.3f, 테스트 R^2: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
'''이차 선형'''
slr = LinearRegression()
slr.fit(X_train_poly, y_train)
y_train_pred = slr.predict(X_train_poly)
y_test_pred = slr.predict(X_test_poly)
print('이차 선형')
print('훈련 MSE: %.3f, 테스트 MSE: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('훈련 R^2: %.3f, 테스트 R^2: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
Mean squared error가 감소하고 $R^2$가 증가한 것으로 보아 fitting이 더 잘 된 것을 볼 수 있습니다. 하지만 주의해야 할 점은 다항식의 차수가 증가할수록 feature 가 증가하는 것이므로 과적합이 발생할 확률이 높다는 것입니다. 이에 따라 적절한 계수를 선택하여 모델 훈련을 진행하여야 합니다.
'Theory > Statistics' 카테고리의 다른 글
| Classification - Logistic Regression (2) (0) | 2021.04.19 |
|---|---|
| Classification - Logistic Regression (1) (0) | 2021.04.18 |
| Regression - 다중공선성 (Multicollinearity) (0) | 2021.04.15 |
| Regression - 다중 선형 회귀 in Python (0) | 2021.04.15 |
| Regression - 다중 선형 회귀 (0) | 2021.04.15 |



