Feature Selection - Random Forest (1)
지난 포스트에서 Random Forest 에서의 Gini impurity를 기반으로 한 feature importance 계산을 알아봤습니다. 그렇다면 계산된 feature importance 를 얼마만큼 신뢰할 수 있을까요?
Example
다음 데이터에 대해 Random Forest 분류/회귀를 수행해보도록 하겠습니다.
먼저 price 열을 RandomForestRegressor 함수로 예측한 뒤 feature importance를 보도록 하겠습니다. 이때 random 이란 열을 만들어 무작위로 값을 넣습니다. Fitting이 되더라도 random 열의 feature importance는 낮아야 합니다.
from sklearn.ensemble import RandomForestRegressor
features = ['bathrooms', 'bedrooms', 'longitude', 'latitude', 'price']
dfr = df[features]
X_train, y_train = dfr.drop('price',axis=1), dfr['price']
X_train['random'] = np.random.random(size=len(X_train))
rf = RandomForestRegressor(
n_estimators=100,
min_samples_leaf=1,
n_jobs=-1)
rf.fit(X_train, y_train)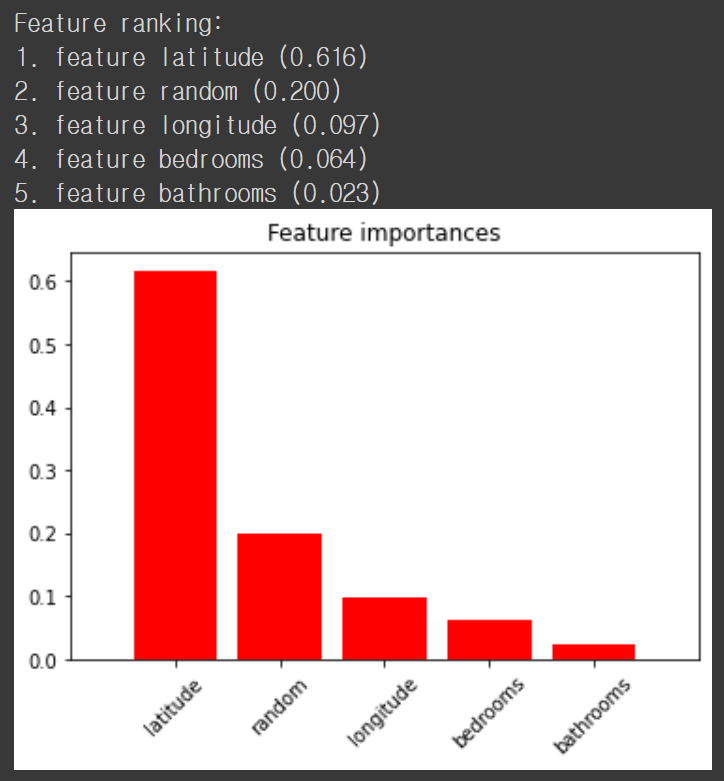
놀랍게도 예측에 전혀 상관이 없어야 할 random 열의 feature importance가 다른 feature에 비해 높습니다. 뭔가 이상합니다. 그렇다면 interest_level 열을 RandomForestClassifier 로 분류하는 모델을 만들고 feature importance 를 보도록 하겠습니다. 이번에도 마찬가지로 random 열을 만들고 랜덤한 값을 넣습니다.
features = ['bathrooms', 'bedrooms', 'price', 'longitude', 'latitude', 'interest_level']
dfc = df[features]
X_train, y_train = dfc.drop('interest_level',axis=1), dfc['interest_level']
X_train['random'] = np.random.random(size=len(X_train))
rfc = RandomForestClassifier(
n_estimators=100,
# better generality with 5
min_samples_leaf=5,
n_jobs=-1)
#oob_score=True)
rfc.fit(X_train, y_train)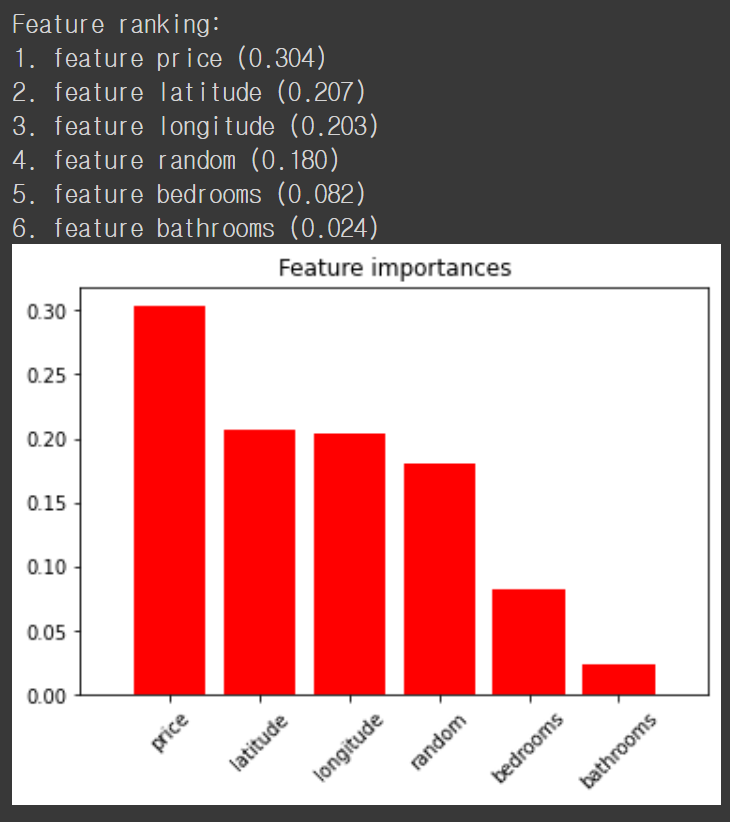
이번에도 비슷한 결과가 나왔습니다. random feature 가 중요도가 있을 수는 있지만 bedrooms/bathrooms 변수보다 중요도가 높다는 것은 말이 안되죠.
Problem
Mean decrease in impurity (Gini impurity) 기반의 feature importance 는 기본적으로 연속형 변수나 많은 범주를 가진 (high-cardinality)를 가진 변수의 importance 를 과대평가하는 경향이 있습니다. 이는 이러한 변수들이 노드 분기의 기준이 될 기회가 많아서라고 생각할 수 있습니다. 예를 들어 분기에 따른 information gain 자체는 적더라도 이러한 변수로 노드 분기 자체가 많아지면 상대적인 importance가 증가하게 되는 것이죠.
물론 여러 수치형 변수를 정규화하고 범주를 줄이는 과정을 통해 어느 정도 해결할 수 있겠지만 의사결정나무 기반의 모델이 이러한 전처리 없이 수행할 수 있는 간편한 모델이라는 것을 생각할 때 꽤나 아쉬운 결과입니다. 그렇다면 어떤 방식으로 해결해야 할까요?
Permutation importance
이러한 상황에서 사용할 수 있는 방법이 바로 해당 변수의 데이터를 임의로 섞는 permutation importance 입니다. 지난 포스트에서는 scikit-learn 패키지의 permutation_importance 함수를 이용했지만 다음과 같이 쉽게 구현이 가능합니다. (여기서는 baseline 성능과 permuted 성능의 차이로 구현했습니다)
def permutation_importances(rf, X_train, y_train, metric):
baseline = metric(rf, X_train, y_train)
imp = []
for col in X_train.columns:
save = X_train[col].copy()
X_train[col] = np.random.permutation(X_train[col])
m = metric(rf, X_train, y_train)
X_train[col] = save
imp.append(baseline - m)
return np.array(imp)또한, permutation importance는 훈련에 쓰이지 않은 데이터에 대해서 측정해야 하므로 Random Forest 를 구성하는 의사결정나무에서 쓰이지 않은 데이터 (out of bag)로 성능을 측정하고 feature importance 를 계산하면,
from sklearn.metrics import r2_score
def oob_regression_r2_score(rf, X_train, y_train):
X = X_train.values if isinstance(X_train, pd.DataFrame) else X_train
y = y_train.values if isinstance(y_train, pd.Series) else y_train
n_samples = len(X)
predictions = np.zeros(n_samples)
n_predictions = np.zeros(n_samples)
for tree in rf.estimators_:
unsampled_indices = _get_unsampled_indices(tree, n_samples)
tree_preds = tree.predict(X[unsampled_indices, :])
predictions[unsampled_indices] += tree_preds
n_predictions[unsampled_indices] += 1
if (n_predictions == 0).any():
warnings.warn("Too few trees; some variables do not have OOB scores.")
n_predictions[n_predictions == 0] = 1
predictions /= n_predictions
oob_score = r2_score(y, predictions)
return oob_score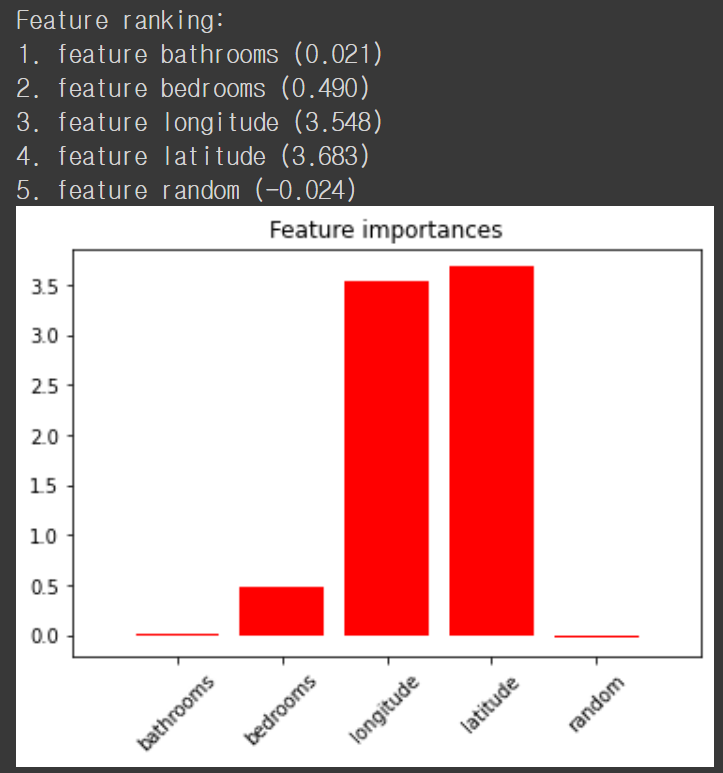
우리가 의도했던 것처럼 random 변수가 제일 중요도가 낮습니다. Random 변수를 무작위로 섞어도 기존과 차이가 없을 것이니 당연합니다. 분류에서도 마찬가지의 결과를 얻을 수 있습니다.
def oob_classifier_accuracy(rf, X_train, y_train):
X = X_train.values
y = y_train.values
n_samples = len(X)
n_classes = len(np.unique(y))
predictions = np.zeros((n_samples, n_classes))
for tree in rf.estimators_:
unsampled_indices = _get_unsampled_indices(tree, n_samples)
tree_preds = tree.predict_proba(X[unsampled_indices, :])
predictions[unsampled_indices] += tree_preds
predicted_class_indexes = np.argmax(predictions, axis=1)
predicted_classes = [rf.classes_[i] for i in predicted_class_indexes]
oob_score = np.mean(y == predicted_classes)
return oob_score
홍머스 정리
- 연속형 이거나 범주의 개수가 많은 high-cardinality 변수일수록 mean decrease in impurity 기반의 feature importance 가 과대평가된다.
- 특히 모델이 과적합되어 지나치게 많은 분기가 이루어질 경우 이러한 현상이 더욱 심해진다. 따라서 제대로된 feature importance를 얻기 위해서는 모델을 과적합시키지 않는 것이 중요하다.
- scikit-learn 에서 기본적으로 제공하는 feature importance 이외에도 permutation feature importance 등의 방법을 같이 고려하여 공통적으로 높은 중요도를 가진 feature 를 선택하여야 한다.
참조
'Machine Learning Models > Classic' 카테고리의 다른 글
| Classification - Metrics (1) (0) | 2021.04.19 |
|---|---|
| Feature Selection - XGBoost (0) | 2021.04.17 |
| Feature Selection - Random Forest (1) (0) | 2021.04.16 |
| Feature Selection - Recursive Feature Elimination (0) | 2021.04.09 |
| Feature Selection - Permutation Feature Importance (0) | 2021.04.09 |



