이번 포스트에서 살펴볼 논문은 IMSAT 과 마찬가지로 mutual information 을 최대화하여 clustering 하는 방법론에 관한 내용입니다. 입력 $x$와 $x$에 대한 출력 $y$의 mutual information 을 최대화하는 IMSAT과 달리 이번 포스트의 IIC (Invariant Information Clustering)에서는 입력 $x$와 $x$와 비슷한 $x'$의 각 출력의 mutual information 을 최대화하는 것인데요, image clustering 과 segmentation 에 적용하여 놀라운 성능을 거두었다고 합니다. 자세한 내용을 한 번 살펴보겠습니다.

Method
Invariant information clustering
먼저 $x, x'$ 을 이미지의 내용이 비슷한 한 쌍의 데이터라 정의합니다. 예를 들어 같은 물체를 담고 있는 서로 다른 이미지 쌍이 있습니다. IIC의 목적은 clustering을 위해 $x, x'$에서 각 이미지 별 고유의 정보 (instance-specific) 대신 공통된 정보만을 추출하도록 하는 $\Phi: X \to Y$를 학습하는데 있습니다. 즉, $\Phi(x')$로부터 $\Phi(x)$를 잘 예측하도록 $\Phi(x)$와 $\Phi(x')$의 mutual information 을 최대화시키도록 학습합니다.
$max_{\Phi} I(\Phi(x), \Phi(x'))$ (Equation 1)
$\Phi$가 clustering 목적으로 출력단의 차원이 제한된 숫자 (cluster 개수 $C$)이므로 Equation 1을 통해서 instance-specfic 한 정보를 제거할 수 있습니다. 왜냐하면 $I(x, x') \geq I(\Phi(x), \Phi(x'))$ 이므로 출력단의 차원의 제한이 없을 경우 Equation 1은 단순히 $\Phi=I$ (identity mapping) 으로 귀결되기 때문입니다. 또한, 출력단의 차원을 cluster 개수로 제한하고 입력이 어떤 cluster 에 속하는지에 대한 확률로 나타내기 위해 (soft clustering) $\Phi$의 마지막에 softmax 를 추가하여 $\Phi(x) \in [0,1]^C$ 가 되도록 합니다. ($P(z=c|x) = \Phi_c (x)$)
$x, x'$에 대한 cluster 할당 변수 $z, z'$를 생각해보면, $x, x'$가 주어졌을 때 $z, z'$가 독립이므로 $P(z=c, z'=c'|x, x')=\Phi_c (x) \cdot \Phi_{c'}(x')$와 같이 표현할 수 있습니다. 이를 배치 단위로 marginalize 했을 때, $z, z'$의 결합확률분포 $P(z, z')$은 $C\times C$ 크기의 행렬로 표현할 수 있습니다.
$P=\frac{1}{n}\sum_{i=1}^n \Phi(x_i)\Phi(x'_i)^T$
따라서 $P$의 $c$번째 행과 $c'$번째 열은 $P_{cc'}=P(z=c, z'=c')$을 나타내고 $P_c = P(z=c), P_{c'}=P(z'=c')$는 $P$의 해당하는 열을 합해서 얻을 수 있습니다. 특히 $(x_i, x'_i)$와 $(x'_i, x_i)$의 대칭성을 표현하기 위해 $P$를 $(P+P^T)/2$로 대칭화해서 사용합니다. 따라서 이를 Equation 1에 대입하고 mutual information의 정의를 사용해서 Equation 2와 같이 표현할 수 있습니다.

Mutual information $I(z, z')=H(z) - H(z|z')$ 이므로 이를 최대화하는 것은 군집 할당 엔트로피 $H(z)$를 최대화하고 $z'$가 주어졌을 때의 $z$의 엔트로피인 $H(z|z')$이 최소화하는 것과 동일합니다. $H(z|z')$가 가질 수 있는 최소값은 0으로 이것은 $z'$이 $z$로부터 확실하게 결정된다는 의미이고 $H(z)$가 가질 수 있는 최대값은 $ln(C)$로 전체 군집분포에서 각 군집의 비율이 동일하다는 것입니다. (uniform 분포)
따라서 mutual information 을 최대화시키는 것을 단순히 엔트로피를 최대화시키는 것과 다릅니다. 단순히 엔트로피만을 최대화시킨다면 출력 $z$가 uniform 분포가 되는 trivial 솔루션으로 귀결되고 이는 어떠한 형태의 군집도 이루어지지 않습니다. 엔트로피 최대화에 조건부 엔트로피 최소화 조건을 추가함으로써 $z'$으로부터 $z$가 확실히 (deterministic) 결정될 수 있도록 합니다.
Image clustering
그렇다면 $x'$을 어떻게 얻을까요? IIC에서는 이미지에 대한 랜덤 tranformation $g$를 정의하여 $x'=gx$를 사용합니다. $g$는 geometric 한 scaling, skewing, rotation, flipping 이거나 contrast, color saturation 과 같은 색상 변화를 이용합니다. (원래의 $x$가 가진 정보를 손상시키지 않는 선에서 어떠한 종류의 변환이 가능합니다.) 따라서 IIC는 $x$와 변환된 $x'$에서 불변의 공통 정보 (invariant) 를 추출하도록 학습되고 이 정보가 cluster를 이루는데 사용됩니다. Pytorch 코드로는 Figure 4와 같이 간단히 구현할 수 있습니다.

STL10과 같은 데이터셋은 두 가지 종류의 훈련 데이터가 존재합니다. 하나는 10개 클래스에 대한 데이터이고 (13K 개) 나머지는 10개 클래스와 관련없는 데이터인데 (100K 개) 수가 더 많은 관계없는 데이터를 활용하기 위해 IIC는 Figure 2와 같은 부가적인 출력단을 (auxiliary head) 하나 더 달아 over-clustering 합니다. 즉, 주 출력단 (main head) 에서는 정해진 군집 개수로 ($k_{gt}$) 훈련시키고 auxiliary head 에서는 $k_{gt}$보다 더 많은 $k$개의 출력단으로 훈련시킴으로써 많은 수의 unlabeled data를 훈련에 포함시켜 사용함으로써 더 좋은 representation 을 추출할 수 있도록 학습합니다.

Image segmentation
Image segmentation 에 대해서도 image clustering 과 근본적으로 비슷하나 1) 예측이 각 픽셀별로 수행되고, 2) 전체 데이터가 아닌 전체 데이터의 부분적인 이미지 패치에 대해 수행되므로 근접한 패치에 대한 invariance가 (local spatial invariance) $x$로부터 $x'$을 생성하는데 사용됩니다.
$x\in R^{3\times H\times W}$ (Pytorch 기준) 를 RGB 이미지, $u\in \Omega = \{ 1, ..., H\} \times \{1, ..., W\}$ 를 픽셀 위치, $x_u$를 $u$를 중심으로한 이미지 패치라 했을 때 IIC를 위한 $(x_u, x_{u+t})$ 이미지 쌍을 구성합니다. 여기서 $t$는 $u$로부터의 displacement $t \in T$를 나타냅니다. 따라서 $\Phi (x_u)=\Phi_u (x) \in [0,1]^C$ 로 나타내고 $\Phi (x)$는 segmentation 이므로 $[0,1]^{C\times H\times W}$의 크기를 갖습니다. 최종적으로 $\Phi_u (x), \Phi_{u+t} (x)$가 IIC에 사용됩니다.
Image clustering 부분에서 설명한 기하학적/색상적 변환 $g$는 각 패치에 대해서 적용될 수 있겠지만 비효율적이므로 전체 이미지에 대해서 선행적으로 진행되는데, 중요한 점은 원래 이미지에서의 픽셀 위치가 변환 이미지 상에서 바뀌므로 이를 서로 맞도록 조정해주어야 한다는 점입니다. 즉, $\Phi_u (x)$가 $\Phi_u (gx)$와 맞지 않게 된다는 것입니다. $\Phi_u (x)$는 $\Phi_{g(u)}(gx)$와 대응되므로 $\Phi(gx)$에 역변환 $g^{-1}$을 가한 $[g^{-1} \Phi (gx)]_u$가 $\Phi_{g(u)} (gx)$와 대응됩니다. 예를 들어 입력을 뒤집었다면 출력 이미지도 뒤집어야 된다는 것이죠. 최종적으로 segmentation 을 위한 IIC 목적함수는 Equation 3과 같습니다.
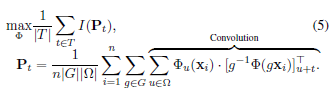
Equation 3은 $\Phi_u (x_i)$와 $[g^{-1} \Phi (gx_i)]_{u+t}$의 mutual information을 최대화하는 것이고 이것이 데이터 개수 $n$, 변환의 종류 $g$, 픽셀 개수 $u$에 대해 평균되어 사용됩니다. (displacement $t$ 에 대해서는 information 을 계산 이후에 평균을 내는 것이 성능이 더 좋다고 합니다.)
그렇다면 Equation 3의 displacement $t$에 대한 구현은 어떻게 이루어질까요? $y=\Phi(x), y'=\Phi(x')$ 에 대해서 먼저 $y'$을 $y$의 좌표로 bilinear resampler를 이용해 되돌립니다. ($y' \leftarrow g^{-1}y'$) 따라서 Equation 3의 안쪽 summation (convolution 이라 표현된 부분)은 두 개의 tensor의 convolution이 됩니다. ($P=y*y'$) 따라서 패딩 크기를 $d$라고 했을 때 $y, y' \in R^{n\times C\times H\times C}$ 이므로 $P\in [0,1]^{C\times C\times (2d+1)\times (2d+1)}$ 로 구해집니다. ($P$를 normalize 합니다.)
다음 포스트
'Machine Learning Tasks > Clustering' 카테고리의 다른 글
| Clustering - Invariant Information Clustering for Unsupervised Image Classification and Segmentation (2) (0) | 2021.05.17 |
|---|---|
| Clustering - Performance (3), S_Dbw (0) | 2021.05.12 |
| Clustering - Performance (2), Total Sum of Squares (0) | 2021.05.12 |
| Clustering - Performance (1) (0) | 2021.05.11 |
| Clustering - Hungrian Algorithm (2) | 2021.05.11 |



