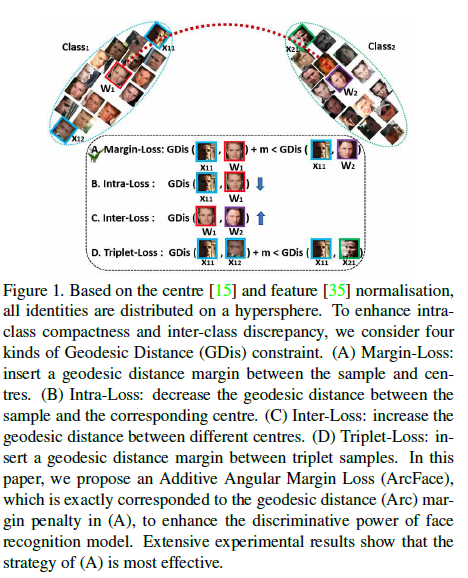
대용량 얼굴 이미지를 기반한 얼굴 인식을 위해서 같은 클래스의 feature 들이 뭉치고 (minimize intra-class variation) 다른 클래스의 feature 들이 펼쳐지는 (maximize inter-class variation) discriminative feature 학습 방법이 많이 제안되었고 대표적으로 1) softmax loss 기반의 방법들과, 2) triplet loss 기반의 방법론이 있습니다. (Figure 1에서의 geodesic 거리란 일반적으로 공간 상에서 가장 짧 표면 거리를 말합니다. 쉽게 예를 들면 지구라는 구 위에서 서울-뉴욕사이의 geodesic 거리는 지구 표면상에서 서울-뉴욕의 최단거리가 되는 것이죠. )
Softmax loss 기반의 방법론은 마지막 fully-connected layer 의 선형 변환 $W\in R^{d\times n}$의 크기가 사람 클래스 수 $n$이 증가할수록 커지며 closed-set 에서는 잘 동작하지만 얼굴 인식과 같은 open-set 프로토콜 하에서는 충분히 discriminative 하지 않습니다. Triplet loss 기반은 클래스 별로 triplet 데이터를 구성해야되기 때문에 훈련 시킬 사람 클래스 수가 많아지면 훈련 시간이 늘어나고 negative 데이터를 잘 뽑아야 된다는 어려움이 있습니다.
특히, SphereFace 는 softmax loss 에 angular 마진이라는 개념을 도입하여 discriminative feature 학습을 가능하게 했습니다. 하지만 SphereFace 는 cosine 각도에 정수 마진을 곱했기 때문에 cosine 값의 주기성을 없애기 위해 단조감소 함수 $\psi$를 대신 사용했고 이 값은 구간 별로 급격히 떨어지다보니 안정된 훈련을 위해 annealing 최적화 기법을 사용했습니다. 따라서 훈련이 어렵고 훈련 초기에는 실질적으로 softmax loss 가 사용되다 보니 최적화된 수렴이 어렵습니다. CosFace 같은 경우는 cosine 값 자체에 마진을 부여한 경우로 SphereFace 보다 구현이 쉽고 더 높은 성능을 얻을 수 있었죠.
ArcFace 에서도 CosFace 와 마찬가지로 feature / weight 벡터를 정규화시키지만 cosine 값에 마진을 부여하는 것이 아닌 arc-cosine 함수를 사용하여 각도 자체에 마진을 부여합니다. 즉, $cos(\theta) \rightarrow cos(\theta+m)$ 식으로 각도에 직접적인 마진을 부여하는 것이죠.
ArcFace
Equation 1의 softmax loss 로부터 시작합니다. $x_i \in R^{d}$에서 $d=512$ 는 feature 차원이고 $W_j \in R^{d\times n}, b_j \in R^n$ 입니다. 이후 기존 방법과 마찬가지로 $b_j=0$ 으로 두면 $W_j^T x_i = \Vert W_j\Vert \Vert x_i\Vert cos(\theta_j)$ 로 표현할 수 있고 $W_j, x$를 정규화하면 Equation 2와 같이 표현할 수 있습니다. 이때, $x$는 크기가 1이 되도록 정규화한 이후에 scale factor $s$를 다시 곱해줍니다. Feature / weight 벡터를 정규화시키는 과정을 통해 예측이 각도에만 의존하며 feature 벡터는 $s$의 크기를 가진 hypersphere 상에 위치합니다.
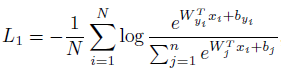
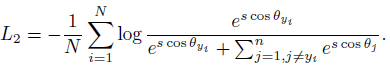
이후 intra-class compactness / inter-class separation 을 위해 마진 $m$을 부여합니다. 이때, cosine 값에 마진을 부여하는 것이 아닌 각도에 마진을 더해줌으로서 geodesic 거리상에 페널티를 부여합니다. (Equation 3) 이를 additive angular margin (AAM) 페널티를 부여했다고 하며 geodesic 거리인 arc 에 페널티를 부여한 것이므로 ArcFace 라 이름짓습니다.
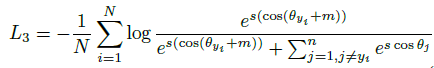
한 명당 1500개의 이미지를 가진 8명에 이미지에 대해 2 차원의 feature 공간 상에서 실험했을 때, Figure 3과 같이 ArcFace 가 각 클래스 중심으로 해당 feature 들이 잘 뭉쳐져 있는 것을 확인할 수 있습니다.

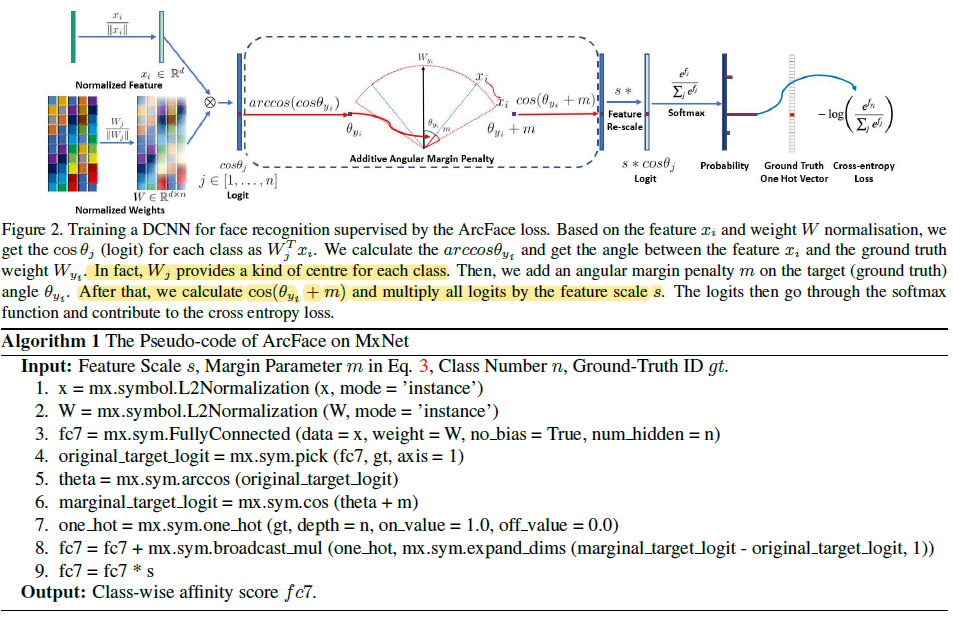
ArcFace 의 전체적인 과정과 알고리즘은 Figure 2와 같습니다. 주목할 점은 arc-cosine 함수로 $x_i, W_j$ 사이의 각도 $\theta_j$를 구한 이후 additive angular 마진을 더하고 다시 cosine 값을 더해준 이후에 $s$를 곱해 feature 크기를 조절합니다.
Comparison with SphereFace and CosFace
SphereFace, ArcFace, CosFace 모두 각기 다른 형태의 마진을 부가합니다. 부가되는 형태는 각각 다르나 모두 intra-class compactness / inter-class separation 을 강제하여 discriminative feature 학습을 위한 것들이죠. SphereFace, ArcFace, CosFace 마진을 각각 $m_1, m_2, m_3$ 로 했을 때, Equation 4와 같이 하나의 수식으로 표현할 수 있습니다.
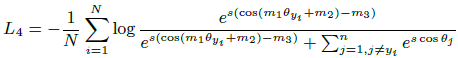
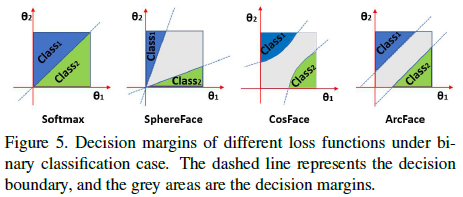
그렇다면 마진이 부가되는 형태에 따라 hypersphere 상의 feature 분포는 어떻게 달라질까요? Figure 5는 이진 분류에 대한 각 loss 의 decision boundary 를 나타내는데 ArcFace 만이 각도에 따라 일관된 마진을 가짐을 알 수 있습니다.
또한, SphereFace 에서 $m_1$을 정수로 강제해 annealing 최적화 기법을 사용했었던것과 달리 CosFace 는 arc-cosine 함수를 사용해서 $m_1$이 실수값을 가지도록 A-Softmax 함수를 재구성했다고 합니다. 그 결과 훈련 초기에 softmax loss 를 사용하는 부가적인 훈련 기법이 필요한 SphereFace 와 달리 안정된 수렴을 보이고 $m=1.35$ 정도에서 최적의 성능을 얻었다고 합니다.
Comparison with other losses
다른 loss 함수들도 feature / weight 벡터의 각도로서 표현할 수 있습니다. 마찬가지로 intra-class compactnesss / inter-class separation 을 강제하는 방식으로 loss 함수를 설계할 수 있는데요, 먼저 Intra-Loss 는 intra-class compactness 를 강제하므로 Equation 2에 feature 와 클래스 중심 사이의 각도 $\theta_{y_i}$를 줄이는 함수를 Equation 5와 같이 추가합니다.
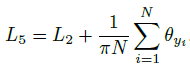
Inter-Loss 는 Intra-Loss 와 반대로 inter-class discrepancy 를 강제하므로 각 클래스 중심간의 각도를 $arccos(W_{y_i}^T W_j)$ 늘리는 함수를 Equation 6과 같이 추가합니다. $\sum_{j=1, j\neq y_i}^n$의 경우수가 $n-1$ 이므로 이를 나눠준 것을 확인할 수 있습니다.
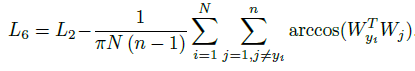
Triplet-Loss 는 triplet 데이터를 구성하는 샘플들간의 각도를 늘리는 것이 목적이므로 정규화된 feature 간의 각도에 마진을 부가합니다. 따라서 $x_i$가 $x_i^{pos}$와의 각도가 마진만큼 더 가까워지도록 Equation 7과 같이 표현할 수 있습니다.
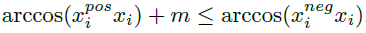
다음 포스트
'Machine Learning Tasks > Face Recognition' 카테고리의 다른 글
| Face Recognition - ArcFace (2) (0) | 2021.05.25 |
|---|---|
| Face Recognition - CosFace (2) (0) | 2021.05.23 |
| Face Recognition - CosFace (1) (0) | 2021.05.23 |
| Face Recognition - SphereFace (2) (0) | 2021.05.22 |
| Face Recognition - SphereFace (1) (0) | 2021.05.21 |



