반응형
문제
정상에 도달하기 위해 $n$ 계단을 올라야 하며, 매번 1 계단 혹은 2 계단씩 오를 수 있습니다. 정상에 도달하기 위한 방법은 몇 가지 경우가 될까요?
1. n=3 => 3- 1) 1+1+1, 2) 1+2, 3) 2+1 의 총 3가지 경우가 있습니다.
풀이
$n=3$인 경우는 간단하니 $n=5$의 경우를 생각해봅시다. 1 혹은 2 계단씩 오를 수 있으므로 5 계단을 오르는 경우의 수를 계산하려면 3 계단을 오르는 경우의 수와 4 계단을 오르는 경우의 수를 합하면 될 것 같습니다. 이런 식으로 반복하다 보면 자연스럽게 생각나는 부분은 다이나믹 프로그래밍입니다.
- 먼저, $n$ 이라는 큰 문제를 $n-1, n-2, n-3...$ 의 작은 문제로 지속적으로 쪼개 나가면서 풀 수 있습니다. 이는 다이나믹 프로그래밍의 최적 부분 구조에 부합합니다.
- 중복된 하위 문제가 있습니다. 5 계단을 오르는 경우, 3 계단을 오르는 경우를 계산하는 부분이 2 번 포함됩니다.
kaggle.com 의 notebook으로 작성한 풀이는 다음과 같습니다.
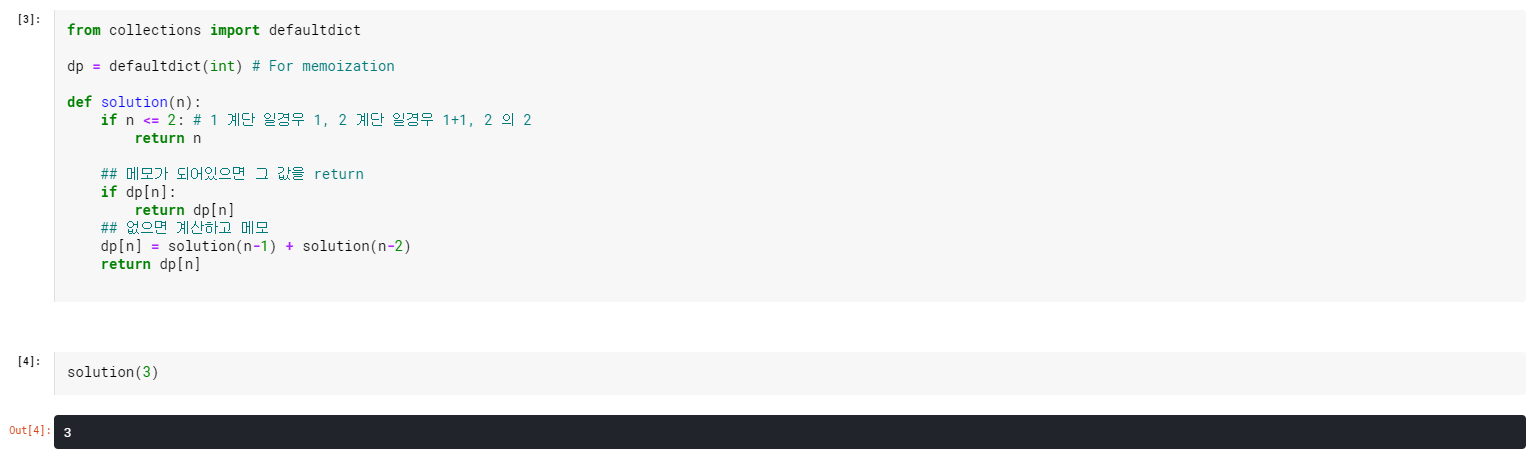
다이나믹 프로그래밍의 메모이제이션 코드와 거의 비슷합니다. return 조건의 경우 $n=1$이면 1가지 경우의 수, $n=2$이면 (1+1, 2)의 2가지 경우의 수가 존재하므로 $n$ 값을 return합니다.
홍머스 정리
- 다이나믹 프로그래밍, 메모이제이션
- 난이도: 하
참조
- <파이썬 알고리즘 인터뷰>, p639-641
반응형
'Computer > Coding Test' 카테고리의 다른 글
| 코딩테스트 문제 (9) - 효율적인 화폐구성 (0) | 2021.02.24 |
|---|---|
| 코딩테스트 문제 (8) - 개미 전사 (0) | 2021.02.24 |
| 코딩테스트 문제 (6) - 연속적으로 반복되는 최대 문자열 길이 (0) | 2021.02.23 |
| 코딩테스트 문제 (5) - 가장 큰 수 (0) | 2021.02.23 |
| 코딩테스트 문제 (4) - 구간 병합 (0) | 2021.02.23 |



