최적화란 기본적으로 주어진 목적함수를 최소화 혹은 최대화시키는 입력을 찾는 과정입니다. 한정된 자원에서의 최대 효율을 달성해야 하는 상황은 공학, 자연과학 분야뿐 아니라 실생활에서도 광범위하게 존재하기에 유관한 대부분의 학과에서 접하게 됩니다. 대표적으로 유전 알고리즘 (Genetic Algorithm), Particla Swarm Optimization, Simulated Annealing, Differential Evolution 등 다양한 meta-heuristic 알고리즘들이 있죠. 주어진 목적이 하나라면 다른 것을 희생시킬 필요가 없기에 간단하지만 한정된 자원에서 두 가지 이상 목적을 충족하려면 어떻게 해야 할까요? 수학적으로 표현하면 다음 $M$개의 목적을 동시에 만족시키고 싶은 겁니다.
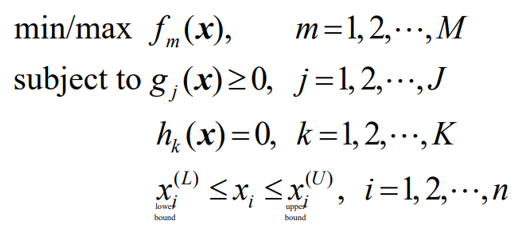
파레토 최적
한정된 자원에서 여러 목적을 만족시키는 것은 경제학의 영원한 숙제죠. 당연히 이와 관련하여 연구가 진행되었고 이탈리아 경제학자 파레토는 파레토 최적화된 상황을 제시합니다. (20%가 80%를 소유한다는 파레토 법칙의 파레토가 맞습니다.) 나무위키에는 파레토 최적화는 "어떤 자원배분 상태가 주어졌을 때, 다른 사람에게 손해가 가도록 하지 않고서는 어떤 한 사람에게 이득이 되는 변화를 만들어내는 것이 불가능한 상황"이라 정의되어 있습니다. 그럼 다음 상황에서 라면을 어떻게 나누면 파레토 최적화 상태일까요?

나무위키를 보면 2명이서 "모두" 라면을 1~2개까지 가질 때 파레토 최적상태라고 나옵니다. 즉, 파레토 상태에서는 누군가의 후생이 증가하면 다른 사람의 후생이 감소하는 상황인 거죠. 여기서부터 알 수 있는 것은 파레토 최적이란 목적이 하나일 때와는 달리 정확히 하나의 답이 있지 않고 균등 분배와도 관련이 없습니다. 파레토 법칙처럼 20명이 80명보다 가진 것이 많은 상황에서 20명의 것을 80명에게 나눠줄 때 20명의 후생이 감소한다면 그 상황 자체가 파레토 최적상태라는 것이죠.
파레토 우위, 열위
파레토 비최적상태는 최적상태와 반대로 무엇인가 변할 때 아무도 손해를 보지 않는 상황입니다. 즉, 후생 총합이 증가하는 상황으로 밑에서 (2.5,0.5) 경우에 라면 0.5개를 나눠주면 아무도 손해를 보지 않고 후생이 증가합니다. 따라서 파레토 최적상태는 어떤 상태가 더 좋은지 비교가 불가능하지만, 파레토 비최적상태에 비해서는 확실히 파레토 최적상태가 "좋다"라고 말할 수 있죠. (좋은 경우는 우위, 나쁜 경우는 열위라고 합니다) 즉, 최적상태끼리의 비교는 불가능하지만 비최적상태끼리는 비교가 가능합니다.

이걸 수식적으로 한 번 봐보겠습니다. 밑의 그림에서 $f_1$은 최대화를 시키고 싶고, $f_2$는 최소화를 시키고 싶습니다. 파레토 최적상태면 파레토 비최적상태에 대비해서 좋기 (우위) 때문에 다른 어떠한 샘플에 대해서라도 파레토 열위를 당하지 않으면 그 샘플이 파레토 최적상태이겠죠.
- 1 vs 2: 1번은 2번에 비해 $f_2$ 값도 낮고, $f_1$은 높습니다. 즉, 완벽한 우위입니다.
- 1 vs 5: 1번은 5번과 비교해 $f_2$ 값은 동일하지만 $f_1$은 낮습니다. 즉, 5번에 의해 열위를 당하니 파레토 최적이 아니겠죠.
- 3 vs 4: 3번은 4번보다 $f_1$ 값도 크고 $f_2$ 값도 작습니다. 따라서 4번은 파레토 최적이 아니겠죠.
- 3 vs 5: 3번은 5번보다 $f_1$ 값은 작지만 $f_2$ 값은 큽니다. 따라서 서로 비교가 불가능합니다.

Multi-Objective 최적화
최적화할 대상이 여러 개인 Multi-Objective 최적화에서는 결국 주어진 입력 공간 상에서 파레토 최적상태인 해를 찾는 과정이라고 볼 수 있습니다. 즉, 어떠한 샘플에 대해서도 파레토 열위를 당하지 않는 샘플들이 해가 되고 언급한 대로 보통 하나가 아닌 여러 개가 동시에 해가 되게 됩니다. 영어로 정의한 파레토 최적해는 다음과 같습니다.
Pareto Optimal Solution
: Given a set of solution, the non-dominated solution set that are not dominated by any member of the solution set

참조
'Theory > Algorithms' 카테고리의 다른 글
| Multi-Objective 최적화 (3) - NSGA-3 (0) | 2023.05.06 |
|---|---|
| Multi-Objective 최적화 (2) - NSGA-2 (0) | 2023.05.05 |
| 자료구조 - 해시 함수와 엔트로피 (0) | 2022.09.09 |
| 자료구조 - 사전과 셋 (Dictionary, Set) (0) | 2022.09.09 |
| 자료구조 - 리스트와 튜플 (List, Tuple) (0) | 2022.08.07 |

