Multi-Objective 최적화 (1) - 파레토 (pareto) 최적
Multi-Objective 최적화 (2) - NSGA-2
NSGA (Non-dominated Sorting Genetic Algorithm)의 종류는 여러 가지가 있으나 각 샘플 별 $n_p, S_p$를 계산하여 파레토 front level 순으로 정렬하는 Non-dominated Sorting은 동일합니다. NSGA-3 알고리즘은 NSGA-2의 같은 front level에 속한 샘플들을 가려내던 crowding distance를 reference direction으로 바꾼 알고리즘입니다.
Reference direction
Reference direction은 $M$개의 목적함수에 대해 다음 조건을 만족하는 $w_i$의 집합입니다. $w_i$에 따라 각 목적 함수의 가중치가 달라지게 되죠. 따라서 $w_i$는 특정 목적 함수에 치중되지 않도록 균등하게 퍼져있게 미리 생성되거나 사용자의 선호도에 따라 사전 정의가 가능합니다. $w_i$를 생성하는 대표적인 방법으로는 Das and Dennis 방법이 있습니다.
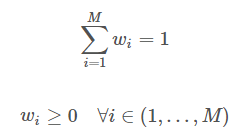
Das and Dennis
$w_i$를 균등하게 생성하기 위해 각 목적 함수의 값이 0에서 1 사이로 스케일링된 unit simplex 구조로부터 출발합니다. 각 목적 함수를 $p$개의 균등한 간격으로 나눈다고 했을 때, $C_p^{M+p-1}$개의 reference point가 샘플링되고 reference direction은 원점으로부터 각 reference point를 연결한 직선이 됩니다. 다음 그림에서처럼 3개의 목적 함수가 있고 $p=3$일 때 $C_3^{3+3-1}=10$개의 포인트 생성이 가능합니다. (그림의 Layer 1)

하지만 Layer 1의 포인트들은 대부분 f1/f2/f3의 unit simplex의 경계에만 위치하게 되어 하나 이상의 목적 함수의 가중치가 0이 되게 됩니다. 따라서 layer-wise 식으로 접근해서 다음 layer는 unit simplex 크기를 줄이고 점은 뽑습니다. 따라서 layer 2 이후에 뽑힌 점들은 원래 크기의 unit simplex 상에서는 경계가 아닌 내부에 위치하게 되는 것이죠. 위의 그림에서는 layer 1/2/3에 대해 각각 $p=3,2,1$을 적용하여 10, 6, 3개의 점을 뽑는데 이 중 9개의 점은 boundary, 나머지 10개의 점은 interior에 위치하게 됩니다.
Das and Dennis 단점
먼저 unit simplex 크기를 줄이는 shrinkage factor를 정하는 것이 애매합니다. 또한 예를 들어 우리가 5개의 목적 함수에 대해 $p=(3,2)$나 $p=(2,2,2,1)$ 두 가지로 50개의 reference point를 만드는 것이 가능한데, 이러면 설계에 따라 unit simplex 상에서의 균등성 (uniformity)가 깨지게 됩니다.
다음으로 우리가 원하는 숫자의 reference point를 정확히 샘플링할 수 없습니다. Das and Dennis 방법에서는 $M=3, p=10$이면 $C_10^{3+10-1}=66$, $p=11$이면 78개의 포인트가 샘플링되어 만약 우리가 70개의 reference point를 원한다면 Das and Dennis 방법으로는 불가능합니다. 또한, $M$이 커진다면 $p$증가에 따른 샘플링 포인트 수는 급증하겠죠.
마지막으로는 $p, M$ 관계에 따라서 unit simplex 상의 interior point 숫자가 달라진다는 점입니다. 특히 $p <M$이라면 interior point가 없고 (위 그림의 Layer 2/3 모든 포인트는 경계에 있습니다.) $p=M$일 경우 1개의 interior point만 생성됩니다. (Layer 1의 가운데 빨간 점) $p> M$인 경우부터 interior point가 생성되기 시작하는데, 전체 샘플링되는 point 수에 비하면 굉장히 작은 부분만을 차지하게 됩니다. 즉, 다음 그림처럼 $p$를 $M$에 비해 굉장히 크게 잡아야 interior point 비율이 늘어나는데, 이렇게 되면 total point 수가 지나치게 많아지게 됩니다. 결국 unit simplex 상에서 균등하게 point를 잡아야 한다는 목적에서 생각해 보면 비효율적일 수밖에 없습니다.
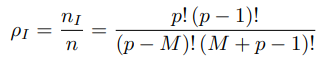

이를 극복하기 위해 다양한 방법들이 고안되었고 자세한 내용은 Multi-Object 최적화 파이썬 라이브러리인 pymoo 홈페이지에서 확인할 수 있습니다. (물론 사용자 편의에 따라 정의된 reference point도 사용 가능합니다.)
NSGA-3
NSGA-3에서는 NSGA-2와 Non-dominated Sorting 부분은 공유하고 같은 파레토 front level에 속한 집합에서 일부를 추출할 때 crowding distance가 높은 샘플 대신 reference direction과 가까이 있는 샘플을 선택합니다. 즉 다음 그림처럼 0-1 사이로 정규화된 목적 함수 공간에서 reference direction과의 수선거리가 가장 짧은 샘플을 선택합니다. (그림의 $W$가 reference direction 입니다.) 따라서 reference point가 unit simplex 상에서 균등하게 분포되어 있다면 crowding distance처럼 파레토 solution 상에서 최대한 다양성을 고려하여 샘플링하는 의미로도 볼 수 있습니다.

참조
'Theory > Algorithms' 카테고리의 다른 글
| Multi-Objective 최적화 (2) - NSGA-2 (0) | 2023.05.05 |
|---|---|
| Multi-Objective 최적화 (1) - 파레토 (pareto) 최적 (1) | 2023.05.04 |
| 자료구조 - 해시 함수와 엔트로피 (0) | 2022.09.09 |
| 자료구조 - 사전과 셋 (Dictionary, Set) (0) | 2022.09.09 |
| 자료구조 - 리스트와 튜플 (List, Tuple) (0) | 2022.08.07 |

