시계열 (Time Series) 데이터는 무엇일까요? 시계열 데이터란 $x_1, x_2, ... , x_n, ...$ 의 확률 변수가 시간 순으로 모아놓은 추계적 과정 (stochastic process)의 일종으로 각 시점의 값은 확률 변수 (random variable)의 realization (관측) 으로 결정됩니다.
우리가 흔히 볼 수 있는 시계열 데이터는 아마도 주가 차트일겁니다. 주가, 경제 지표 등 시간의 순으로 나열된 값들의 지표는 시계열 데이터라 볼 수 있고 우리는 이러한 시계열 데이터를 통해
- 시계열의 패턴을 요약하여 시간에 따른 상관관계, 추세, 계절성 등의 특징을 파악하고
- 과거의 패턴이 미래까지 지속된다는 가정 하에 미래 시점에 대한 예측을 하고자 합니다.
이번 포스트에서는 시계열 분석을 위해 필요한 기본적인 확률 개념을 알아보도록 하겠습니다.
확률
확률을 정의하기 위해서는 표본 공간 (sample space), 사건 (event) 를 정의해야 합니다.
표본 공간이란 어떤 특정 실험을 수행하였을 때, 측정 가능한 모든 결과들의 집합을 말합니다. 또한, 표본 (sample) 이란 표본 공간을 이루는 각각의 결과를 말하며, 표본은 표본 공간의 부분집합이 됩니다. 예를 들어 동전을 2번 반복해서 던지는 실험을 할 때, 표본 공간은 {(앞,앞),(앞,뒤),(뒤,앞),(뒤,뒤)} 로 구성되겠죠.
사건 (event)는 표본 공간의 부분집합으로 어떤 조건을 만족하는 표본의 집합입니다. 예를 들어, 동전을 2번 던져 모두 앞이 나올 조건을 기다린다고 했을 때, (앞,앞)이 나온다면 바로 사건이 발생한 것입니다.
확률은 그럼 다음과 같이 정의할 수 있습니다. 동일한 조건 하에서 동일한 실험을 무수히 많이 반복하여 실행할 때, 어떤 특정한 사건 (A) 가 발생하는 비율입니다. 다음과 같이 정의될 수 있습니다.
$P(A) = \frac{A 사건이 일어나는 경우의 수}{모든 사건이 일어나는 경우의 수}=\frac{A 사건 안의 표본 개수}{표본 공간의 표본 개수}$
확률 변수 (random variable)
확률 변수란 표본 공간안의 각각의 표본들을 실수 공간의 특정한 수치적 값으로 표현한 변수를 말합니다. 예를 들어 동전을 두 번 던져 앞이 나온 횟수를 세는 실험을 수행한다고 생각해봅시다. 그렇다면 표본 공간은 {(앞,앞),(앞,뒤),(뒤,앞),(뒤,뒤)로 구성되며, 이때 앞이 나온 횟수 $X$ 는 0, 1, 2의 실수로 표현할 수 있습니다. 이 $X$를 확률 변수로 하고 확률 변수를 통한 값 $R$은 ${0,1,2}$가 되어 상태 공간이라 불립니다. 결과적으로 확률 변수는 표본 공간에서 실수 공간으로 표본을 mapping하는 함수로 볼 수 있습니다.

확률 변수는 변수가 취하는 값이 모든 실수값을 택하는 연속확률 변수와 0,1,2... 와 같은 분리된 값만 택하는 이산확률 변수로 구분할 수 있습니다.
확률 분포 (probability distribution) 와 확률 함수 (probability function)
확률 분포란 확률 변수의 모든 값과 그에 대응하는 확률이 어떻게 분포하고 있는지를 말합니다. 확률 함수는 확률 변수가 정의한 값 (X) 에 대해 확률 값 (Y)을 대응시키는 함수를 말합니다. 우리가 아는 Gaussian distribution, Laplace distribution 등이 있습니다. 특정 실험의 표본 공간으로부터 확률까지의 관계는 다음 그림과 같이 표현할 수 있습니다.

PDF (Probability Density Function), CDF (Cumulative Distribution Function)
PDF는 위에 언급한 확률 함수를 말합니다. 특정 확률 변수 값에 대응하는 확률을 mapping하는 함수입니다. CDF는 확률 변수가 $X$ 어떤 변수 $x$보다 작을 확률을 말하고 $P(X\leq x) = F_X (x)$ 라 표기합니다. 2개의 확률 변수 $X,Y$에 대한 CDF는 $P(X\leq x, Y\leq y) = F_{XY} (x, y)$로 표현합니다. CDF를 알면 해당 확률 변수의 모든 특성을 다 알 수 있으며, 이를 특정 값에 대해 미분했을 때, 특정 값에 대한 확률을 알 수 있습니다. 따라서 CDF를 알면 자연스럽게 PDF 또한 알 수 있게 됩니다.
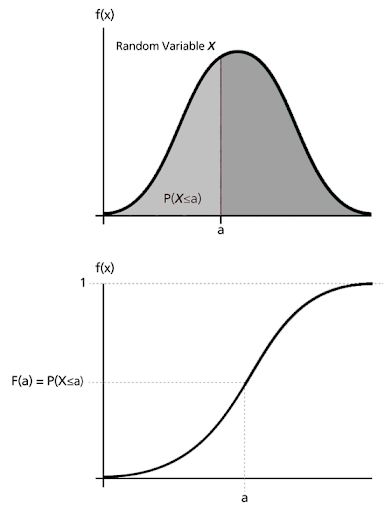
확률 변수 통계
확률 변수 및 확률 분포는 다양한 통계적 정의로 측정되어집니다. 대표적으로 평균, 분산 등이 있습니다.
평균 (Mean, Expectation)
평균이라 하면 단순히 산술 평균을 떠올리기 쉽지만 확률에서의 평균은 확률 변수의 값이 가질 수 있는 기대값으로 보통 expectation의 $E$를 통해 표기합니다. 밑의 식은 이산 확률 변수에 대한 기대값으로 $\sum$으로 계산하였지만 연속 확률 변수에 대한 기대값은 적분 ($\int$)로 계산합니다.
$Expectation = E[X] = \sum_{i} x_i * p_i$
분산 (Variance)
분산은 확률 변수와 확률 변수의 평균의 차의 제곱의 평균으로 해당 확률 변수가 얼마나 넓게 분포되어 있는지 나타내는 지표입니다. 기대값 $E[X]=\mu$라 한다면,
$Variance X = E[(X-E[X])^2] = E[(X-\mu)^2]$
$E[X^2 - 2E[X]*\mu + \mu^2] = E[X^2] - \mu^2$
위의 식에서 볼 수 있듯이 분산은 확률 변수의 제곱의 평균에서 평균의 제곱의 차로 구할 수 있습니다. 위 수식에서 상수 $a$에 대해 $E[aX]=aE[X]$인 기대값의 성질을 이용하였습니다.
n차 모멘트 (n-th Moment)
분산에서는 확률 변수의 제곱이 사용되었습니다. 이를 확장하여 확률 변수에 대한 3제곱, 4제곱 통계치를 구할 수 있고 이를 확률 변수의 n차 모멘트라 합니다. 평균은 0에 대한 1차 모멘트, 분산은 평균에 대한 2차 모멘트라 할 수 있습니다. 특히, 평균에 대한 3차 모멘트는 비대칭도 (Skewness), 평균에 대한 4차 모멘트는 첨도 (Kurtosis)라 하며 (확률 분포의 꼬리 부분의 두께, 값이 높으면 heavy-tailed), 분산 처럼 0에 대한 모멘트를 알면 쉽게 구할 수 있습니다.
공분산 (Covariance)
공분산은 2개의 확률 변수에 ($X, Y$) 대해서 각 확률 변수가 서로에 대해 선형적으로 얼마나 관계를 가지는지를 측정하는 지표이며, $Cov(X,Y)$ = $E[(X-E[X])(Y-E[Y])$ = $E[XY] - E[X]E[Y]$ 로 계산됩니다.
공분산의 특징을 몇 가지 특징을 알아보면,
1) 자기 자신의 공분산은 분산이 됩니다. ($Cov(X,X) = E[(X-E[X])(X-E[X])] = E[(X-E[X])^2$),
2) 공분산이 0보다 크다면 $X, Y$는 양의 선형관계를 가지고 0보다 작다면 음의 선형관계를 가지고,
3) 공분산이 0이라면 $X, Y$는 성현관계를 가지고 있지 않으며,
4) $X, Y$가 서로 독립이라면 $Cov(X,Y) = E[XY]-E[X]E[Y] =0$이 되지만 역은 성립하지 않습니다. 공분산이 0이라 해도 $X, Y$가 선형 관계만 없을 뿐이지 독립은 아닙니다. 예를 들어 $Y=X^2+1$의 관계를 가진 $X,Y$에 대해서는 선형관계가 없으므로 공분산은 0이지만 서로 관계를 가지고 있으므로 독립이 아닙니다.
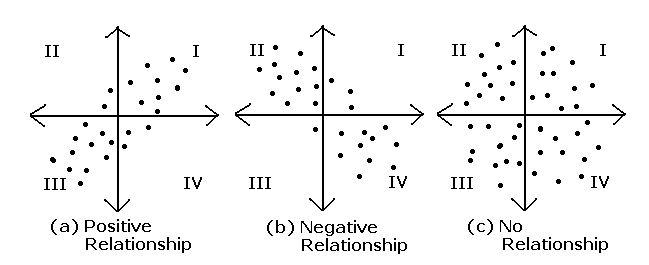
상관계수 (Correlation)
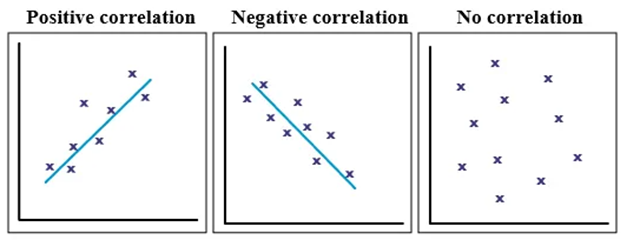
상관계수는 공분산이 $X, Y$의 크기 단위에 영향을 받으므로 이를 공정히 비교하기 위해 공분산을 정규화 한 것입니다. 즉, 확률 변수의 절대적 크기에 영향 받지 않기 위해 단위화 한 것으로서 각 확률 변수의 분산의 크기만큼 나누어 준 것입니다. 상관계수는 공분산을 정규화 한 것이니만큼 -1부터 1까지의 값을 가지며, 공분산과 마찬가지로 양수이면 양의 선형관계, 음수이면 음의 선형관계를 가진다고 볼 수 있습니다.
$\rho_{XY} = \frac{Cov(X,Y)}{\sqrt{Var(X)} \sqrt{Var(Y)}}$
'Machine Learning Tasks > Time Series' 카테고리의 다른 글
| 시계열 모델 building (0) | 2021.03.10 |
|---|---|
| Partial Correlation (0) | 2021.03.10 |
| Linear model, Autoregressive model, ARMA (0) | 2021.03.08 |
| Autocorrelation, 시계열 분해, Trend estimation (0) | 2021.03.07 |
| 기본 개념 (2) - Stationary, White noise (0) | 2021.03.07 |


