Autocorrelation function (ACF)
지난 포스트에서 autocovariance function $\gamma_X (h) = Cov(X_t, X_{t+h})$ 로 정의하였습니다. 공분산을 풀어쓰면 $Cov(X_t, X_{t+h})$ = $E[X_t X_{t+h}] - E[X_t]E[X_{t+h}]$ 이고 시계열 데이터는 일반적으로 평균이 0이 되도록 shifting 시킬 수 있기 때문에 (이를 demean 혹은 centering 이라 합니다.) $\gamma_X (h) = E[X_t X_{t+h}]$로 볼 수 있습니다. 앞으로 편의상 시계열 데이터의 평균은 0으로 가정하겠습니다.
공분산에서의 상관계수와 마찬가지로 확률 변수의 스케일에 무관하게 하기 위해 autocorrelation function (ACF) 을 다음과 같이 정의할 수 있습니다.
$\rho_X (h) = \frac{\gamma_X (h)}{\sqrt{\gamma_X (0)}{\sqrt{\gamma_X (0)}}} = \frac{\gamma_X (h)}{\gamma_X (0)}$
이것도 상관계수와 마찬가지로 -1에서 1까지의 값을 가지고 있고 이를 통해 autocovariance function의 다음과 같은 특성을 알 수 있습니다.
- $\rho_X (h) = \frac{\gamma_X (h)}{\gamma_X (0)} \leq 1$ 이므로 $|\gamma_X (h)| \leq \gamma_X (0)$ 을 만족합니다.
- $\gamma_X (h) = \gamma_X (t+h - h) = Cov(X_{t+h}, X_t)$ 이고 $\gamma_X (h) = \gamma_X (t - (t-h)) = Cov(X_t, X_{t-h}) = \gamma_X (-h)$ 이므로 $\gamma_X (h) = \gamma_X (-h)$ 를 만족합니다. 즉, 래그 $h$의 부호에 상관없이 대칭성을 가지게 됩니다.
시계열 decomposition
일반적으로 시계열 데이터는 추세 (trend, $m_t$), 계절성 (seasonality, $s_t$)과 stationary한 나머지 성분 (residual) 으로 ($y_t$) 구성되어 있습니다. 원래의 시계열 데이터에서 이 성분들을 각각 쪼개서 추정하는 것이 용이하기 때문에 이것이 더하거나 ($X_t = m_t + s_t + y_t$), 곱해서 ($X_t = m_t * s_t * y_t$) 시계열 데이터를 분석합니다. 결과적으로 시계열 데이터에서 추세와 계절성을 제거한 나머지 성분은 시간 별 의존성이 제거된 stationary white noise 라 가정하여 가정하여 추정하게 됩니다.

추세 (trend)
데이터가 장기적으로 증가하거나 감소할 때, 추세가 존재한다고 합니다. 추세는 반드시 선형일 필요가 없으며, 어떤 추세가 증가하거나 감소하는 경우에 추세의 방향이 변했다고 합니다. 밑의 그림 처럼 아래로 내려가는 추세가 분명히 있다고 판단할 수 있습니다.

계절성 (seasonality)
해마다 어떤 특정한 때나 1주일마다 특정 요일에 나타나는 것과 같은 계절적 요인이 시계열에 영향을 줄 때, 계절성이 있다고 합니다. 계절성은 보통 빈도의 형태로 나타나는데 계절성의 빈도는 보통 일정하다고 알려져 있습니다.
보통 경제 상황과 같은 주기성 (cycle) 도 따지기도 합니다. 고정된 빈도가 아닌 주기가 증가하거나 감소하는 모습을 띌 때 주기 패턴이 나타납니다. 보통 주기성은 계절성에 비해 패턴의 길이가 길고 주기의 크기 또한 변동성이 심합니다. 보통 시계열이 아주 길지 않는 이상 주기성은 생략되기도 합니다. 밑의 그림에서는 강한 계절성과 더불어 증가하는 추세를 확인할 수 있습니다.
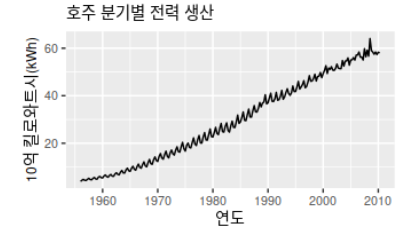
Trend estimation
일반적으로 시계열 데이터를 다루기 위해서는 추세와 계절성을 데이터상에서 제거해서 stationary 한 나머지 부분 ($y_t$)만 남겨 다룰 수 있도록 합니다. 먼제 추세를 어떻게 시계열에서 예측하고 stationary 한 부분만 남길 수 있을까요? 예측한 추세를 $\hat{m_t}$라 하면 다음 4가지 방법이 있습니다.
Smoothing with a finite moving average filter
이 방법은 특정한 윈도우 안의 신호들의 평균으로 시계열 데이터를 smoothing 시키는 방법입니다. Nonseasonal 시계열 데이터 $X_t = m_t + y_t$ 가 있다고 가정하고 특정 양수 $q$에 대해서 다음 smoothing된 신호를 새로 정의할 수 있습니다.
$w_t = \frac{1}{2q+1} \sum_{i=-q}^{i=q} X_{t-q}$
$\hat{m_t} = w_t = \frac{1}{2q+1} \sum_{i=-q}^{i=q} m_{t-i} + \frac{1}{2q+1} \sum_{i=-q}^{i=q} y_{t-i}$
위의 수식에서 오른쪽 y에 관련된 항은 랜덤성에 의해 0에 근접할 것이라 예상할 수 있고 왼쪽 m에 관련된 항은 m이 선형 추세를 가지고 있다면 자기 자신 $m_t$에 의해 가까워 질 겁니다. ($\hat{m_t}$) $q$를 조절하면서 추세를 찾을 수 있습니다. 또한, 밑의 그림처럼 윈도우 크기를 크게 잡을수록 신호가 더 부드러워 지게 됩니다.

Exponential smoothing
Moving average를 이용한 smoothing은 특정 윈도우 안의 신호를 평균을 내어야 하기 때문에 윈도우 사이즈 만큼의 지연 시간이 발생합니다. 즉, weighted moving average 의 일종으로 전 시점과 지금 신호 값의 가중 평균을 통해 추세를 구하는 방법입니다. Exponential smoothing 은 $\alpha$를 조절해가며 추세를 찾아갑니다.
$\hat{m}_t = \alpha x_t + (1-\alpha) \hat{m}_{t-1}, \hat{m}_t=x_1$
Smoothing splines
Spline은 점과 점 사이를 3차원 이상의 다항식으로 연결하는 방식으로 3차원 다항식으로 연결할 경우 cubic splines 이라 합니다. 3차원인 이유는 각 구간 접점의 미분 값이 같아지도록 만들어서 자연스럽게 모든 점을 연결할 수 있는 최소 차수이기 때문입니다.
각 점 사이를 각각의 3차원 다항식으로 잘 연결할 수 있으나 점들을 그대로 따라가기 때문에 추세를 놓칠 수가 있습니다. 따라서 splines으로 이은 이후 이를 부드럽게 만들어주기 위한 (smoothing) regularizer가 필요합니다. $f_t$를 각 3차원 다항식의 t 시점에서의 값이라 한다면 smoothing splines는 다음 식을 최소화 함으로써 얻어질 수 있습니다.
$\sum_{t=1}^{n} (x_t - f_t)^2 + \lambda \int (f''_t)^2 dt$
왼쪽 항은 splines이 각 점을 잘 표현할 수 있다도록 하는 항이고 오른쪽 항은 splines가 얼마나 부드러운지 조절하는 regularizer 항이고 $\lambda$ 를 통해 조절합니다. $\lambda$가 클수록 연결한 선이 더 부드러워 지게 되고 $\lambda$를 level of smoothness 라 합니다.
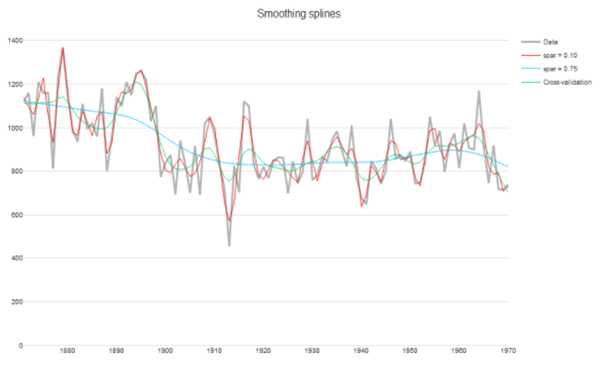
Kernel smoothing
Kernel smoothing은 moving average의 일종인데 전 시간점의 각 계수를 kernel function을 통해 weight를 달리하는 방법입니다.
$\hat{m_t} = \sum_{i=1}^{i=n} w_i (t) X_i$
즉, t에 대해 영향을 미치는 전 시간점들을 특정 weight ($w_i (t)$) 로 주어서 t에 대해 미치는 영향력을 모델링합니다. (Moving average의 단순한 산술 평균과는 다릅니다.) Kernel의 종류는 다양하지만 일반적으로 가우시안 kernel 을 사용하며, weight는 다음과 같이 결정됩니다.
$w_i (t) = K(\frac{t-i}{b}) / \sum_{j=1}^n K(\frac{t-j}{b}), K(z) = \frac{1}{\sqrt{2\pi}} exp(-\frac{z^2}{2})$
시점 $t$에 대해 생각해보면 t에 가까운 지점의 weight는 먼 지점에 비해 더 크게 됩니다. 이때, $b$는 bandwidth로 영향의 폭을 조절하는 파라미터로 $b$가 커지면 먼 지점의 영향력이 상대적으로 더 커지고 반대로 $b$가 작아지면 먼 지점의 영향력은 상대적으로 감소하게 됩니다. 따라서 $b$가 커지면 더 부드러운 smoothing 결과를 얻을 수 있습니다.
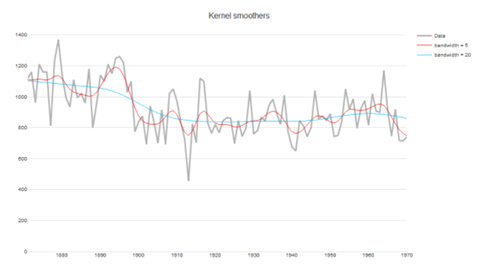
Trend elimination by differencing
이 방법은 각 시점의 차를 이용해서 추세 성분을 제거하는 방법입니다. $Z_t = X_t - X_{t-1} = m_t - m_{t-1} + y_t - y_{t-1}$ 인데, 추세가 선형이라면 $m_t - m_{t-1}$은 상수가 되고 $y_t$가 stationary 하다면 $Z_t$가 stationary 하게 됩니다.
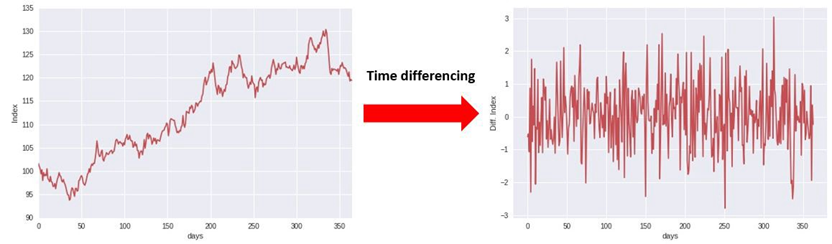
차이를 하는 것은 시계열 분석에 굉장히 많이 사용하기 때문에 backshift operator $B$를 다음과 같이 사용합니다.
$BX_t = X_{t-1}, B^{2}X = X_{t-2}, B^{3}X = X_{t-3}, ...$
$B$를 이용해 차이를 표현하면 $\nabla X_t = X_t - X_{t-1} = (1-B)X_t$, $\nabla^2 X_t = \nabla\nabla X_t = \nabla ((1-B)X_t) = (1-B)^2 X_t$ 와 같이 표현할 수 있습니다. 일반화하면 $\nabla^d = (1-B)^d$로 표현할 수 있습니다.
'Machine Learning Tasks > Time Series' 카테고리의 다른 글
| 시계열 모델 building (0) | 2021.03.10 |
|---|---|
| Partial Correlation (0) | 2021.03.10 |
| Linear model, Autoregressive model, ARMA (0) | 2021.03.08 |
| 기본 개념 (2) - Stationary, White noise (0) | 2021.03.07 |
| 기본 개념 (1) - 확률 (0) | 2021.03.07 |


