비선형 활성화 함수는 deep neuarl networks 설계에 필수적인 요소입니다. 초창기에는 sigmoid, tanh 같은 함수가 주로 사용되었지만 bounded 되어있는 특성상 gradient 포화현상이 발생하여 현재는 ReLU 함수가 거의 대부분의 (특히, CNN 계열의) neural networks 에서 대표적인 비선형 활성화 함수로 사용되고 있습니다.
ReLU (Rectified Linear Unit) 은 sigmoid, tanh 함수에 비해 일반화 성능 및 수렴 속도가 좋다고 알려져 있지만 만능의 함수는 아닙니다. ReLU 의 대표적인 문제로는 dying ReLU 로서 이는 ReLU 함수 자체가 음수값을 아예 0으로 만들어버리기 때문에 값이 한번 음수가 되버리면 그 부분에 대해서는 기울기 또한 0이 되어 훈련이 되지 않는 현상입니다. 이를 극복하기 위해 음수 부분을 살짝 다르게한 Leaky ReLU, ELU, SELU 등이 등장하였지만 ReLU 에 비해 성능향상이 거의 미미하고 데이터셋이나 모델에 따라 성능향상이 일관되지 않아 주로 사용되지 않는 실정입니다.
이번 포스트에서 소개해 드릴 내용은 Mish 활성화 함수입니다. 먼저 Mish 함수는 구글에서 발표한 Swish 함수에 기초하고 있고 Swish 함수는 $f(x) = x\cdot sigmoid(\beta x)$로 정의됩니다. 여기서 $\beta$는 훈련 가능한 파라미터로 $\beta=0$이면 identity 함수, $\beta=\infty$면 ReLU가 됩니다. Swish 함수의 모양은 Figure 1과 같은데, ReLU 함수와 같이 unbounded above, bounded below 형태를 가지지만 중요한 차별점은 Swish 함수는 모든 점에서 미분가능하고 단조증가함수가 아니라는 점입니다.

Mish 함수는 Swish 함수를 연장하여 $f(x)=x\cdot tanh(softplus(x))$ 형태를 정의합니다. ($softplus(x) = ln (1+e^{x})$) Swish, Mish 함수와 같이 자기자신 $x$에 비선형 함수를 거친 값을 곱한 것을 self-gating 이라 하는데 이는 LSTM 에서의 gating 모델링에서 유래된 것입니다. 이렇게 자기자신으로부터 스스로 gating 을 수행하니 다른 활성화함수와 마찬가지로 pointwise 함수로 사용될 수 있어 쉽게 치환이 가능합니다. Mish, Swish 형태의 활성화함수는 Figure 2와 같이 다양하게 정의할 수 있지만 CIFAR-10 데이터셋에 대한 간단한 실험시 Mish 함수가 제일 안정적이고 성능이 제일 높습니다.

Mish
Mish 함수를 미분하면 Equation 1과 같이 Swish 함수 형태로 유도할 수 있습니다. $x\cdot sigmoid(x)$는 Swish 함수이며 $sech^2 (softplus(x))=\triangle (x)$ 입니다. 기울기값을 그대로 보존하는 ReLU 함수와 달리 Mish 함수는 $\triangle (x)$가 최적화 과정에서 기울기를 smooth 하게 만들어 수렴을 더욱 쉽게 해주는 preconditioner 로서 동작합니다.

Mish 함수는 Swish 함수와 마찬가지로 1) 단조함수가 아니며, 2) 모든 구간에서 미분가능하고 (smooth), 3) 작은 음수의 값을 보존합니다. (Figure 3) 작은 음수의 값을 보존함으로써 Dying ReLU 값을 설계선에서부터 방지할 수 있습니다. 또한, ReLU 와 마찬가지로 unbounded above 이므로 값이 포화되지 않아 기울기가 사라지는 현상을 방지하고 bounded below 이므로 neural network 파라미터가 값이 급격하게 증가하지 않게 해주는 정규화 효과를 가지고 있습니다.

특히, Mish 함수는 ReLU 함수와 달리 모든 구간에서 연속이고 미분가능합니다. (continuosly differentiable) 이 특징은 기울기 기반으로 파라미터를 업데이트하는 최적화에서 기울기가 정의되지 않아 발생하는 불안정한 요소를 제거하여 neural networks 가 깊어지더라도 정보 손실을 최대한 방지하고 전 layer 로 전파하는 역할을 수행합니다. 이로서 깊은 neural networks 에 대해서도 안정적인 훈련과 높은 성능을 달성할 수 있습니다. Figure 4와 같이 랜덤하게 초기화된 5-layer neural networks 출력을 각 활성화 함수 별로 분석해봤을 때, ReLU 함수의 출력은 급격히 변하지만 Mish 함수의 출력은 굉장히 부드러운 분포를 가지고 있으며 이를 통해 최적화가 상대적으로 용이할 것임을 유추할 수 있습니다.

Figure 5와 같이 CIFAR-10 데이터셋에 200 epoch 만큼 훈련된 ResNet-20 networks 의 loss 분포를 각 활성화 함수 별로 분석해봤을 때, ReLU 함수는 loss 값이 높고 local minima 가 여기저기 산재해 있지만 Mish 함수는 다른 함수에 비해 loss 분포가 낮으면서도 굉장히 부드럽고 넓은 minima 를 가지고 있습니다.

Mish 함수의 특징을 정리하면 Table 1과 같습니다. 정리하면 1) unbounded above 이므로 sigmoid, tanh 함수와 같이 값이 포화되었을때 기울기가 사라지지 않고, 2) 모든 구간에서 미분가능한 smooth 함수이므로 최적화 측면에서 유리하며 파라미터 초기화나 learning rate 에 덜 민감하고, 3) bounded below 이므로 정규화 효과를 가지면서 단조함수가 아닌 특성상 작은 음수부분에 대한 값을 유지하므로 ReLU 함수와 달리 기울기가 없어져버리는 현상을 방지합니다.

Comparison
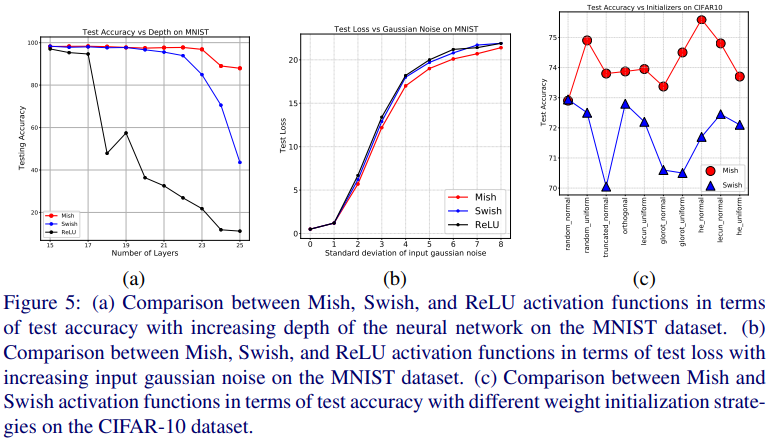
MNIST 데이터셋에 대한 Mish, Swish, ReLU 함수의 성능은 Figure 6과 같습니다. 먼저 Figure 6(a)에서 layer 수가 많아지면 ReLU 함수의 성능은 급격히 늦아지지만 Mish 함수는 성능 감소가 거의 없었으며 이는 smooth 함수인 Mish 특성 상 정보를 잘 전달하기 때문이라 추측됩니다. Figure 6(b)에서는 입력 데이터에 가우시안 노이즈를 첨가했을 때의 loss 그래프로 Mish 함수가 일관되게 낮은 loss 를 가짐을 확인할 수 있습니다. 마지막으로 Figure 6(c)는 neural networks 의 초기화 방법에 따른 성능 추이인데 Mish 함수가 Swish 함수에 비해 초기화 방법에 따라서도 일관되게 우수한 성능을 가짐을 알 수 있습니다.
Benchmarks
Image classification
먼저, CIFAT-10 데이터셋에 대해 Squeeze Net 모델로 다양한 활성화 함수에 대해 여러번 성능을 측정하여 통계적인 유의성을 확보합니다. 단순히 몇번 돌려서 성능이 잘 나왔다기 보다는 통계적으로 유의마한 결과를 얻기 위해서죠. 활성화 함수만 바꾼채 최적화함수 (Adam), epoch 수 (50) 등을 일정히 유지한 채 23번 실험한 결과는 Table 1과 같습니다. 평균 정확도는 ($\mu_{acc}$) Mish 함수가 제일 높고 loss, 정확도의 편차는 Mish 함수가 매우 낮은 편에 속합니다.

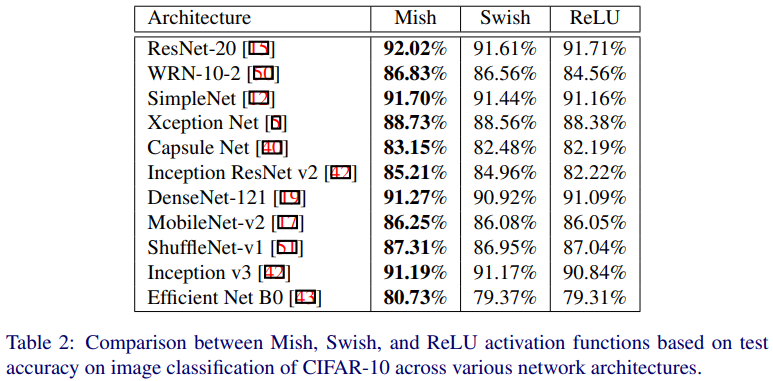
Table 2는 CIFAR-10 데이터셋에 대한 이미지 분류 성능 결과입니다. 하나의 구조가 아닌 다양한 CNN 계열 구조에 대해 실험했으며, Mish 함수가 다양한 구조에 대해서 다른 활성화 함수에 비해 일관되게 높은 성능을 가지고 있음을 알 수 있습니다.
ImageNet 데이터셋에 대한 결과는 Table 3과 같습니다. Mish 함수는 기존에 쓰이던 Leaky ReLU / ReLU 함수에 비해 성능이 더 우수했으며, 간혹 Swish 함수가 성능이 더 높은 경우도 있지만 CSP-ResNext-50 경우에서 데이터 augmentation 을 사용하지 않았을 때 성능이 급격히 감소하는 현상을 보입니다. 이는 Swish 함수가 다양한 모델, 특히 모델이 깊어질수록 성능향상이 일관되지 않음을 나타냅니다.

Object detection
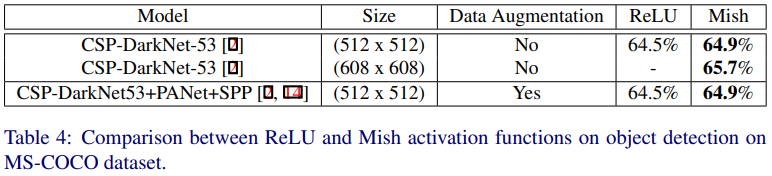
MS-COCO 데이터셋에 대한 object detection 성능은 Table 4와 같습니다. 성능 측정시 detection head 를 제외하고 CSP-DarkNet-53 backbone network 에 대해서 ReLU 함수를 Mish 함수로 대체하여 훈련합니다. 특히, YOLO v4 detector 에 대하여 Mish 함수를 사용함으로써 최소 0.9% 이상의 일관된 AP 향상을 얻을 수 있었다고 합니다. (Table 5)

Pytorch implementation
공개된 official implementation 에는 Pytorch 를 비롯한 다양한 딥러닝 framework 에 대한 Mish 함수 구현체가 존재합니다. 특히, 간단한 비선형 함수이므로 다음과 같이 쉽게 구현할 수 있습니다.
class Mish(nn.Module):
def __init__(self):
super().__init__())
print('Mish activation')
def forward(self, x):
x = x * (torch.tanh(F.softplus(x))
return x
참조
'Machine Learning Models > Techniques' 카테고리의 다른 글
| Label Smoothing (0) | 2021.06.15 |
|---|---|
| CutMix (0) | 2021.06.10 |
| Learning Deep Features for Discriminative Localization (CAM) (0) | 2021.05.08 |
| Interpretable Explanations of Black Boxes by Meaningful Perturbation (0) | 2021.03.16 |
| FLOPS (FLoating point OPerationS) - 플롭스 (2) | 2021.02.25 |



