이번 포스트에서는 시계열 데이터에서 자주 쓰이는 'airline-passengers.csv' 데이터에 대해 Pytorch 프레임워크의 LSTM 모듈을 이용하여 시계열 예측을 수행해보도록 하겠습니다.
Import libraries
먼저 필요한 라이브러리를 호출합니다.
import torch
import torch.nn as nn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from torch.autograd import Variable
from sklearn.preprocessing import MinMaxScaler
Load data
판다스의 'read_csv' 함수를 이용해 데이터를 읽습니다. csv 데이터의 첫번째 열은 날짜이므로 두번째 열만 데이터로 설정하고 min-max 스케일링을 수행합니다.
training_set = pd.read_csv('/content/drive/MyDrive/Time Series/Data/international-airline-passengers.csv')
training_set = training_set.iloc[:,1:2].values
sc = MinMaxScaler()
training_data = sc.fit_transform(training_set)이후에는 시계열 데이터이므로 몇 개의 타임스텝을 현재 시점에 반영할 것인지 정합니다. 즉, 현재 시점의 값은 지정한 시퀀스 길이에 맞게 직전 몇 개의 값과 연관되게끔 데이터를 재구성하는 것이죠.
def sliding_windows(data, seq_length):
x = []
y = []
for i in range(len(data)-seq_length-1):
_x = data[i:(i+seq_length)]
_y = data[i+seq_length]
x.append(_x)
y.append(_y)
return np.array(x),np.array(y)
seq_length = 4
x, y = sliding_windows(training_data, seq_length)이제 훈련 / 테스트 데이터셋을 2:1 비율로 나누어주고 autograd 모듈의 Variable을 이용하여 텐서로 만들어줍니다. 훈련 데이터의 X, y는 각각 [92, 4, 1] / [92, 1] 크기가 됩니다.
Model
이제는 시계열 데이터 모델링을 위한 LSTM 모델을 구현해줄 차례입니다. LSTM (Long Short-Term Memory) 는 입력 시퀀스의 타임 스텝 $t$에 따라 hidden state $h_t$, cell state $c_t$에 따른 출력을 Equation 1과 같이 계산합니다. Equation 1의 $i_t, f_t, g_t, o_t$는 각각 input, forget, cell, output 게이트이며 $\sigma$는 sigmoid 함수를 말합니다.
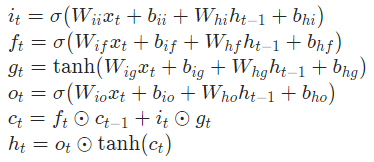
Pytorch 에서는 torch.nn 모듈에서 LSTM 클래스를 쉽게 호출할 수 있습니다. LSTM 클래스 생성시 필요한 파라미터는 다음과 같습니다. "num_layer" 아규먼트를 통해 Multi-layer LSTM을 쉽게 구성할 수 있으며 "num_layer"가 2 이상일 경우, 타임스텝 $t$, layer $l$에 대한 입력으로는 ($x_t^l, l \geq 2$) $h_t^{l-1}$에 dropout이 적용된 텐서가 적용됩니다.
| Parameters | Description |
| input_size | 입력 $x$의 feature 차원 |
| hidden_size | hidden feature 차원 |
| num_layers | LSTM 층의 개수로 2 이상일 경우 Multi-layer LSTM이 됩니다. |
| bias | 디폴트는 True로 설정되어 있고 bias 항을 추가할지 말지를 결정합니다. |
| batch_first | 디폴트는 False로 설정되어 있고 True일 경우 입력, 출력 모두 [배치 사이즈, 입력 길이, feature 차원] 으로 구성되고 False일 경우 입력, 출력 모두 [입력 길이, 배치 사이즈, feature 차원]이 됩니다. 이러한 텐서 차원 순서는 hidden / cell state 에는 적용되지 않습니다. |
| dropout | 마지막 layer의 출력을 제외하고 dropout을 적용합니다. |
LSTM 모델을 사용할 때 주의할 점은 각 타임스텝 별로 hidden / cell state 가 업데이트되는 구조로 동작하기 때문에 초기 $h_0, c_0$를 목적에 맞게 선언해줄 수 있다는 점입니다 각각 [$D$*num_layers, 배치 사이즈, feature 차원] 크기로 되어있고 $D$는 bi-directional 일 경우 2, one-directional 일 경우 1이고 따로 제공되지 않을 경우 디폴트는 0으로 할당됩니다. 또한, 입력, 출력의 텐서 구조는 "batch_first" 아규먼트가 True / False 여부에 따라 배치 차원이 어디에 위치할지 결정됩니다. 일반적으로 배치 차원은 맨 앞에 있는 것이 편리하므로 "batch_first=True"로 설정하는 것이 낫습니다.
LSTM 모델에 대해서 forward 함수를 진행할 경우 출력은 "output, $(h_n, c_n)$" 이 됩니다. 출력텐서는 ("output") "batch_first" 아규먼트에 따라 True일 경우 [배치 사이즈, 입력 길이, $D$*feature 차원] 으로 구성되며 각 타임스텝 $t$에 따른 마지막 LSTM layer의 $h_t$를 담습니다. $h_n, c_n$의 크기는 [$D$*num_layers, 배치 사이즈, feature 차원] 으로 구성되며 마지막 타임스텝의 hidden / cell state가 담깁니다. 모델의 구현은 다음과 같습니다.
class LSTM(nn.Module):
def __init__(self, num_classes, input_size, hidden_size, num_layers):
super(LSTM, self).__init__()
self.num_classes = num_classes
self.num_layers = num_layers
self.input_size = input_size
self.hidden_size = hidden_size
self.seq_length = seq_length
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size,
num_layers=num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, num_classes)
def forward(self, x):
h_0 = Variable(torch.zeros(
self.num_layers, x.size(0), self.hidden_size))
c_0 = Variable(torch.zeros(
self.num_layers, x.size(0), self.hidden_size))
# Propagate input through LSTM
ula, (h_out, _) = self.lstm(x, (h_0, c_0))
h_out = h_out.view(-1, self.hidden_size)
out = self.fc(h_out)
return out- $h_0, c_0$는 hidden / cell state의 초기값이기 때문에 requires_grad=False로 설정된 zero 텐서를 넣어줍니다.
- 현재 시퀀스 길이는 4이고 마지막 시퀀스에 대해 fully-connected layer를 달아주고 싶기 때문에 $h_n$에 대하여 fully-connected layer를 진행시킵니다.
- LSTM 모델의 결과로 나오는 "output"의 마지막 타임스텝 값은 $h_n$과 같습니다.
Train
모델 훈련 시에는 회귀를 위한 MSE loss 함수와 Adam 옵티마이저에 대해 훈련시킵니다. 이 경우에는 훈련 데이터셋의 개수가 92개로 매우 적으므로 전체 데이터에 대해 여러 번 훈련시킵니다.
num_epochs = 2000
learning_rate = 0.01
input_size = 1
hidden_size = 2
num_layers = 1
num_classes = 1
lstm = LSTM(num_classes, input_size, hidden_size, num_layers)
criterion = torch.nn.MSELoss() # mean-squared error for regression
optimizer = torch.optim.Adam(lstm.parameters(), lr=learning_rate)
#optimizer = torch.optim.SGD(lstm.parameters(), lr=learning_rate)
# Train the model
for epoch in range(num_epochs):
outputs = lstm(trainX)
optimizer.zero_grad()
# obtain the loss function
loss = criterion(outputs, trainY)
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print("Epoch: %d, loss: %1.5f" % (epoch, loss.item()))
Test
테스트 진행 시에는 전에 선언했던 "MinMaxScaler" 객체의 "inverse_transform" 함수를 이용하여 원래 데이터 값으로 복원시킵니다.
lstm.eval()
train_predict = lstm(dataX)
data_predict = train_predict.data.numpy()
dataY_plot = dataY.data.numpy()
data_predict = sc.inverse_transform(data_predict)
dataY_plot = sc.inverse_transform(dataY_plot)
plt.axvline(x=train_size, c='r', linestyle='--')
plt.plot(dataY_plot)
plt.plot(data_predict)
plt.suptitle('Time-Series Prediction')
plt.show()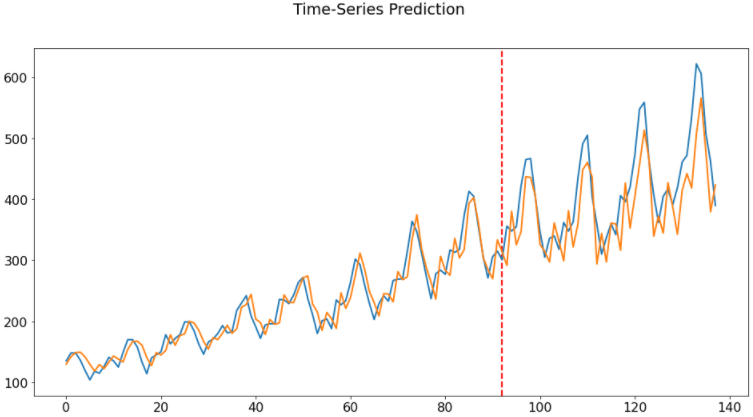
'Machine Learning Models > Pytorch' 카테고리의 다른 글
| Pytorch - ModuleList vs List (0) | 2021.08.09 |
|---|---|
| Pytorch - backward(retain_graph=True) (2) (1) | 2021.08.01 |
| Pytorch - embedding (0) | 2021.06.23 |
| Pytorch - autograd 정의 (1) | 2021.06.02 |
| Pytorch - gather (0) | 2021.06.01 |


