Pytorch - backward(retain_graph=True) (2)

Pytorch - backward(retain_graph=True) (1)

---

일반적으로 손실 함수 (loss function)을 계산할 때는 배치에 대하여 평균/합 등을 통해 스칼라 값을 만들어준 이후에 .backward() 함수를 적용합니다. 스칼라 로스에 대한 각 파라미터 별 기울기를 계산하고 최적화를 수행하죠. 하지만 출력 $y$가 스칼라가 아닌 다변수 벡터 $y=<y_1, ..., y_m>$인 경우에는 .backward() 함수를 어떻게 적용할 수 있을까요? Pytorch에서는 JVP (Jacobian Vector Product)를 계산하여 최종 loss에 대한 파라미터 기울기를 계산합니다.

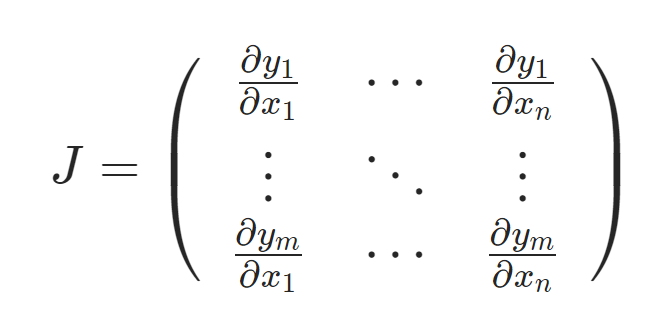
먼저 입력 벡터 $x=<x_1, ..., x_n>$, 출력 벡터 $y=<y_1, ..., y_m>$에 대해서 Figure 1과 같은 Jacobian matrix를 구성할 수 있습니다. 이 상황에서 Pytorch는 Jacobian matrix $J$를 명시적으로 계산하는 것이 아니라 .backward() 함수의 인자로 들어온 벡터 $v$와의 JVP $J\cdot v$를 계산합니다.

Figure 1

출력 벡터 $y=<y_1, ..., y_m>$은 결국 최종 스칼라 로스 $l$을 계산하기 위해 사용됩니다. 즉, Figure 2와 같이 $l$에 대한 $y$의 미분 벡터 $v$를 정의하고 이를 .backward(v) 함수의 인자로 넣어주면, Figure 3과 같이 $l$에 대한 파라미터 $x$의 기울기를 계산하게 됩니다. $J$를 명시적으로 계산하지 않고 우리가 원하는 JVP $J\cdot x$를 계산해주는 것이죠. 당연히 $v$는 $m$ 크기를 가진 벡터 $v=<v_1, ..., v_m>$여야만 합니다. 이러한 방식으로 Pytorch에서는 스칼라가 아닌 벡터 출력에 대해서도 외부에서 정의한 기울기를 집어넣을 수 있습니다. 

Figure 2

Figure 3

 

Example

다음 코드의 출력 "out"은 (5,5) 크기를 가지며, backward() 함수의 인자로 (5,5) 크기를 가지면서 값이 1인 행렬을 넣어준 것을 확인할 수 있습니다. 더 생각해보면 우리가 일반적인 스칼라 값에 대해 .backward() 함수를 수행할 때 .backward(torch.tensor(1.0)) 을 수행한 것과 동일하다는 것을 알 수 있습니다.

import torch

inp = torch.eye(5, requires_grad=True)
out = (inp+1).pow(2)
out.backward(torch.ones_like(inp), retain_graph=True)
print("First call\n", inp.grad)
out.backward(torch.ones_like(inp), retain_graph=True)
print("\nSecond call\n", inp.grad)
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print("\nCall after zeroing gradients\n", inp.grad)

여기서 retain_graph=True를 사용하여 .backward() 함수를 두번째 호출했을 때 기울기가 첫 번째 기울기와 다릅니다. 이는 .backward() 함수를 호출할 때 계산된 기울기를 리프 노드의 grad 속성에 담긴 기존 기울기에 더하면서 누적시키기 때문으로 제대로된 최적화를 수행하기 위해서는 리프 노드의 기울기를 0으로 만들어줘야 합니다.

 

참조

• https://towardsdatascience.com/pytorch-autograd-understanding-the-heart-of-pytorchs-magic-2686cd94ec95
• https://pytorch.org/tutorials/beginner/basics/autogradqs_tutorial.html