이번 포스트에서는 다변수 시계열 데이터 분석을 위한 기본 확률 개념을 알아보도록 하겠습니다.
Multivariate time series
이전 포스트들에서는 단변수 시계열 데이터를 다뤘습니다. 다변수 시계열 데이터는 한 개가 아닌 여러 개의 feature로 구성된 데이터로 하나의 시점에서 스칼라 값이 아닌 다음과 같이 벡터로 표현됩니다.
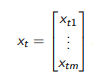
여기서 $m$은 데이터의 feature 차원이 되겠죠. 먼저 평균은 다음과 같이 각각의 기대값이 쌓아진 벡터로 표현됩니다.
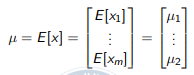
Covariance matrix
Covariance는 다변수이기 때문에 값이 아닌 행렬로 주어집니다. 단변수의 경우 1x1 matrix이기 때문에 스칼라 값이 되는 것이죠. Covariance matrix는 $\sum_X=[Cov(X_i,X_j)]_{i,j}$로 표현되어 $m\times m$ 행렬이 됩니다.
Covariance는 정의에 의해 $E[(X-\mu)(X-\mu)^T]$ 이고 이를 풀어쓰면 $E[XX^T]-\mu\mu^T$가 됩니다. 여기서 T는 전치 행렬을 표시하는 기호입니다. $X, \mu$가 $m\times 1$이고 $X^T, \mu^T$는 $1\times m$이 되어 최종적으로 $m\times m$ 행렬이 되고 $i,j$의 원소는 $Cov(X_i, X_j)=E[(X_i-\mu_i)(X_i-\mu_j)]$가 될 것입니다. 또한 눈여겨봐야 될 특징은 covariance matrix는 symmetric한 ($i,j$ 원소와 $j,i$ 원소의 값이 같은) 대칭 행렬이 되게 됩니다.
$y=Ax$ 에 대해서 $y$ 변수의 covariance matrix는 $x$ 변수의 covariance matrix와 어떤 관계를 가질까요? $\mu_y$=$A\mu_x$ 을 이용하면 다음과 같은 관계를 알 수 있습니다.
$\sum_y$ = $E[(y-\mu_y)(y-\mu_y)^T]$ = $AE[xx^T]A^T - \mu_y\mu_y^T$=$A(E[xx^T]-\mu_x\mu_x^T)A^T$=$A\sum_x A^T$
위 식을 통해서 알 수 있는 것은 covariance matrix 는 대칭 행렬이므로 $x$ 의 어떠한 선형 변환 $A$를 취한 다변수 $y$ 또한 대칭 행렬이 된다는 점입니다. (이를 보통 positive semi-definite 하다 합니다)
Covaraince matrix의 대각선 원소만을 취한 $D=diag(\sum_x)$ 행렬을 만들면 대각선 원소들은 각각 $Var(X_1)$, $Var(X_2)$, $..., Var(X_m)$이 되며 대각선 바깥에 있는 원소들은 0이 되게 됩니다. $D$를 이용해 $D^{-1/2}XD^{1/2}$ 행렬을 생각해보면 $i,j$ 원소는 $\frac{Cov(X_i, X_j)}{\sqrt{Var(X_i)}\sqrt{Var(X_j)}}$ 가 되어 이는 correlation matrix 가 됩니다.
Stationary
다변수 시계열 데이터가 stationary 하기 위해서는 어떠한 조건이 필요할까요? 이도 단변수 시계열 데이터에서 보았던 경우와 똑같습니다. 1. 평균 벡터가 시간 $t$ 에 의존하지 않고 2. $\Gamma(h)$=$Cov(x_{t+h}, x_t)$=$E[(x-{t+h}-\mu_{t+h})(x_t-\mu_t)^T]$ 또한 시간에 의존하지 않아야 합니다. 이때, stationary 하다면 $\mu=\mu_{t+h}=\mu_t$로 생각할 수 있습니다. 주의할 점은 $\Gamma (h) = \Gamma(-h)^T$ 가 됩니다. 단변수 경우에서는 차원이 1이므로 전치 행렬과 본 행렬이 자연스럽게 같게 되어 $\gamma (h) = \gamma (-h)$ 가 되는 것입니다.
정리하면 $\gamma_{i,j} (h)$ = $Cov(X_{t+h,i},X_{t,j})$ 인 $\Gamma (h) = Cov(X_{t+h}, X_t)=[\gamma_{i,j} (h)]_{i,j=1,...,m}$ 이 되고 다변수 시계열에서의 ACF는 래그 h 에 따른 스칼라 값이 아닌 행렬을 다루게 됩니다.
Correlation은 어떻게 될까요? 마찬가지로 $X_{t+h,i}$, $X_{t,j}$에 대해 $\rho_{i,j} (h)$ = $Corr(X_{t+h,i}, X_{t,j})=\frac{Cov(X_{t+h,i}, X_{t,j})}{\sqrt{Var(X_{t+h,i})}\sqrt{Var(X_t,j)}}$ 임을 알 수 있고 이를 확장해서 $[\rho_{i,j} (h)]_{i,j=1,..m}$를 원소로 가진 행렬로 표현할 수 있습니다.
'Machine Learning Tasks > Time Series' 카테고리의 다른 글
| Augmented Dickey-Fuller Test - Stationary 확인 (0) | 2021.03.30 |
|---|---|
| Deep State Space Models for Time Series Forecasting (0) | 2021.03.18 |
| Exponential Smoothing, CMA, Winter's Method (0) | 2021.03.12 |
| Nonstationary process, ARIMA, SARIMA (0) | 2021.03.11 |
| Parameter Estimation, Model Redundancy, Prediction (0) | 2021.03.10 |


