시계열 데이터 예측은 각종 산업의 의사 결정 단에서 두루 사용되는 분야로 비용 감소, 재고 관리 등의 업무에 사용됩니다. 기존에는 예측 모델의 구조를 미리 가정하고 추세나 계절성 등의 패턴을 예측하는 state space models (SSM)이 주로 사용되었습니다만, 사용가능한 시계열 데이터의 수와 feature가 많아짐에 따라 적절한 모델과 입력/출력 구조를 정의하는데 오랜 시간이 걸립니다. 또한, 각 시계열 데이터마다 별도로 모델링되다 보니 비슷한 시계열 데이터들의 공통된 패턴을 활용하지 못하는 단점도 있습니다.
이에 반해 deep neural networks를 사용한 예측은 deep neural networks의 강력한 feature extraction에 힘입어 raw 데이터로부터 복잡한 패턴을 손쉽게 추출할 수 있습니다. 하지만 black-box 모델 특성 상 예측 모델의 구조를 별도로 정의하지 않기 때문에 해석하기가 어렵고 smoothness 같은 제약 조건을 반영하기가 어렵습니다.
이 논문에서는 SSM과 recurrent neural networks (RNN)을 합쳐 둘의 장점을 취하는 방법을 제안합니다. 입력 $x_{1:T}$에 대해서 관측 $z_{1:T}$를 설명하기 위한 SSM의 파라미터를 RNN을 통해서 구하고 이를 통해 예측함으로써 RNN의 복잡한 feature extraction과 SSM의 모델 정의로부터 파생되는 유연함 및 interpretability를 동시에 얻을 수 있습니다.
Background
먼저 문제를 정의하겠습니다. 관측치 $z_{1:T_i}^i, i=1,..,N$은 단변수 시계열 데이터로 covariate 입력 벡터 $x_{1:T_{i+\tau}}$와 연관되어 있습니다. ($z_t \in R, x_t\in R^D$) 시계열 예측의 목표는 관측되지 않은 시점부터 $T_i+1$ 예측하고자 하는 horizon까지 $T_i+\tau$ 관측치 $z_{T_i+1:T_i+\tau}$를 확률적으로 예측하는 것입니다.

위 수식의 $\Phi$는 RNN의 파라미터로 $N$개의 시계열 데이터에 모두 공유됩니다.
State space models
SSM은 시계열의 패턴을 데이터의 크기, 추세, 계절성 등을 encode한 잠재 state $l_t \in R^L$을 통해 모델링합니다. $l_t$는 state-transition dynamic ($p(l_t|l_{t-1})$)으로 모델링되어 시간에 따라 변하게 됩니다. 또한, 관측은 $l_t$로 부터 $p(z_t|l_t)$의 조건부 확률로 정의합니다.
선형 SSM은 다음과 같이 잠재 state의 시간에 따른 변화를 transition matrix $F_t$와 innovation strength $g_t$로 모델링합니다. 즉, $p(l_t|l_{t-1})$ 은 $F_t$와 $g_t$에 의해 latent space에 어떠한 시계열 패턴이 담길지 선형적으로 정의되는 것이죠.

관측 $z_t$는 $t-1$ 시점의 latent space $l_{t-1}$에 의해 다음과 같이 univariate Gaussian 관측 모델로 정의됩니다. 이때, 초기 $l_0$는 isotropic Gaussian 분포 $N(\mu_0, diag(\sigma_0^2))$를 따른다고 가정하며, $a_t\in R^L$, $\sigma_t \in R_{>0}$, $b_t\in R$은 시간에 따라 변하는 파라미터입니다. 또한, $\sigma_t$는 시간에 따라 변화는 관측 노이즈로 볼 수 있습니다.

간단한 level-trend 모델 (선형 추세를 가진 모델)을 생각해 볼때, 시계열의 level, 하나는 trend의 기울기를 나타내는 2차원의 latent state를 생각해 볼 수 있습니다. 시계열 데이터의 $t$ 시점의 level은 $t-1$ 시점의 level과 trend의 기울기로 나타내어지므로 다음과 같이 모델링할 수 있습니다. $l_0$ $\sim$ $N(\mu_0, diag(\sigma_0^2))$일 때, SSM의 모델 파라미터 $\alpha_t, \beta_t, \mu_0, \sigma_0, b_t, \sigma_t$는 RNN에 의해 예측됩니다.

계절성을 지니는 패턴에 대해서는 계절과 관련된 팩터로 모델링할 수 있습니다. 예를 들어 1주일의 사이클일 경우는 7, 매일 사이클일 경우는 1로 latent space의 차원을 잡을 수 있습니다. 이때, RNN이 예측해야 하는 모델 파라미터는 $\gamma_t, \mu_0, \sigma_0, b_t, \sigma_t$가 됩니다.

Parameter learning
SSM은 파라미터 셋 $\Theta_t = (\mu_0, \sigma_0, F_t, g_t, a_t, b_t, \sigma_t)$으로 모델링 됩니다. 일반적으로 이 파라미터들을 추정하는 방법은 marginal likelihood $p_{SS}(z_{1:T}|\Theta_{1:T})$를 최대화 하는 것입니다.

기존의 setting에서는 파라미터가 시간에 불변한 $\Theta_t=\Theta$ 를 가정하였으며 $\Theta^i$가 시계열 데이터 각각에 대해 추정되었습니다. 이에따라 다른 시계열 데이터의 정보를 공유할 수 없어 많은 historical data가 있는 경우에 효율적으로 사용할 수 없습니다.
Deep state space models
Deep state space models은 $x_{1:T_i}$로부터 $\Theta_t^i$을 RNN의 파라미터 $\Phi$를 통해 다음 그림과 같이 mapping 합니다. 밑의 그림을 보시면 입력으로부터 RNN의 LSTM 모델이 state space의 파라미터를 예측이고 예측된 파라미터로 $p_{SS}$가 계산됩니다. 위에 언급한 marginal likelihood $p_{SS}$를 최대화함으로써 RNN의 파라미터 $\Phi$가 학습됩니다.

이때, 마지막 LSTM 층에서 나온 출력은 SSM의 파라미터 도메인으로 affine 매핑됩니다. $t$ 시점의 RNN 출력 $o_t\in R^H$ 일때, $\tilde{\theta}_t=w_\theta o_t + b_\theta$를 계산한 후 SSM 파라미터가 가져야 하는 조건에 맞게 다음과 같이 변환됩니다. 정리하면, RNN의 출력을 그대로 SSM의 파라미터로 사용하는 것이 아니라 $\theta$마다 존재하는 $w_\theta, b_\theta$를 통해 affine transformation을 취한 후에 밑의 조건에 따라 변환해서 사용합니다.

Training
$x_{1:T}$와 $\Phi$가 주어졌을 때, $z_{1:T_i}$ marginal likelihood를 다음과 같이 나타낼 수 있습니다.

따라서 deep state space model의 훈련은 시계열 데이터 셋 ${z_{1:T_i}^i}_{i=1}^N$에 대해 다음의 likelihood를 최대화함으로써 진행됩니다.

Log 안에 있는 각 시계열 데이터에 대한 likelihood는 linear-Gaussian SSM 가정 상에서 Kalman filtering으로 계산할 수 있습니다. Filtering이란 현재 시점까지의 관측치가 모두 주어졌을 때의 latent space의 분포를 찾는 것을 말하며 이는 $p(l_{t-1}|z_{1:t})=N(l_{t-1}|f_t, S_t)$ 의 Gaussian으로 정의됩니다. 여기서 $f_t, S_t$를 Kalman filtering으로 찾을 수 잇습니다. $f_t, S_t$의 분포를 통해 $z^i$의 각 시간별 likelihood를 다음과 같이 계산할 수 있습니다.
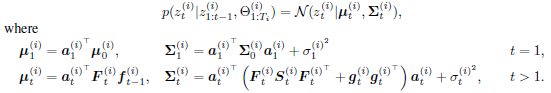
이를 통해 neural networks의 일반적인 stochastic gradient optimization을 통해 $\Phi$를 훈련시킬 수 있으며, likelihood를 계산하는 방법이 기존 SSM의 방법과 근본이 같다보니 SSM의 다른 모델에 대해서도 RNN의 출력을 재정의함으로써 쉽게 확장할 수 있습니다.
Prediction
다시 돌아와 훈련을 마친 RNN을 ($\Phi$) 통해 다음을 예측합니다.

예측 범위 $T_i+1:T_i+\tau$에 대해 multivariate Gaussian인 $p(z_{T_i+1:T_i+\tau})$의 결합분포를 다음과 같이 Monte-Carlo sample로 예측합니다.

Monte-Carlo sample을 생성하기 위해 latent space의 posterior 분포 $p(l_T|z_{1:T})$를 Kalman filtering으로 구한 뒤 이 분포에서 $l_T$를 샘플링하고 RNN을 통해 예측한 파라미터로 latent space transition과 관측 모델을 통해 예측 범위의 샘플을 $K$ 번 생성합니다. 이때, 예측 범위에 대한 입력이 존재한다고 가정합니다.

예측하는 workflow는 다음과 같습니다.
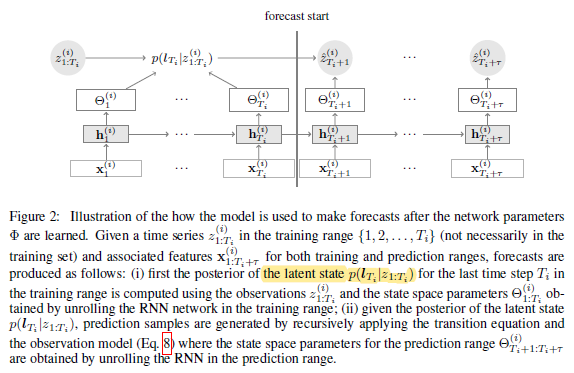
논문에서의 deep state space model은 auto-regressive 모델과 다르게 관측치가 입력으로 들어가지 않습니다. 이로 인해 1) 노이즈에 가장 영향을 많이 받는 관측치가 likelihood 목적 함수에만 관계되 있으므로 모델이 노이즈에 강건하고, 2) 관측치가 없을 경우 목적 함수에서 없는 항만 제거하면 되며, 3) RNN의 unrolling step을 시퀀스 전체에 한 번만 수행하면 되는 이점이 있습니다.
Experiment
Qualitative experiments
가상의 시계열 데이터에 대하여 모델이 파라미터를 RNN을 통해 얼마나 잘 복원하는지 실험합니다. 1주 단위의 계절성을 가지는 그룹마다 모델로 각 초기화 값을 다르게 하여 총 5 그룹의 가상의 시계열 데이터를 생성하였습니다. 예측하여야 할 파라미터는 $\Theta_t=(\mu_0, \sigma_0, \gamma_t, \sigma_t)$이며 $\sigma_t$는 모든 시계열 데이터에 대해 동일하게 하고 $b_t=0$으로 세팅합니다.
각 그룹에서 $N={20,40,140}$개의 시계열 데이터를 사용하였을 때 얼마나 잘 복원하는지는 다음 그림과 같습니다. $N=140$일 수록 파라미터 복원이 거의 정확해지며, $\mu_0$는 쉽게 복원가능한 것을 볼 수 있습니다. 하지만 관측 노이즈 $\sigma_t$와 $\sigma_0$는 상대적으로 복원하기 어려운 것을 확인할 수 있습니다. 밑의 그림의 열은 state space의 각 파라미터이며 줄은 5개의 그룹을 나타냅니다.
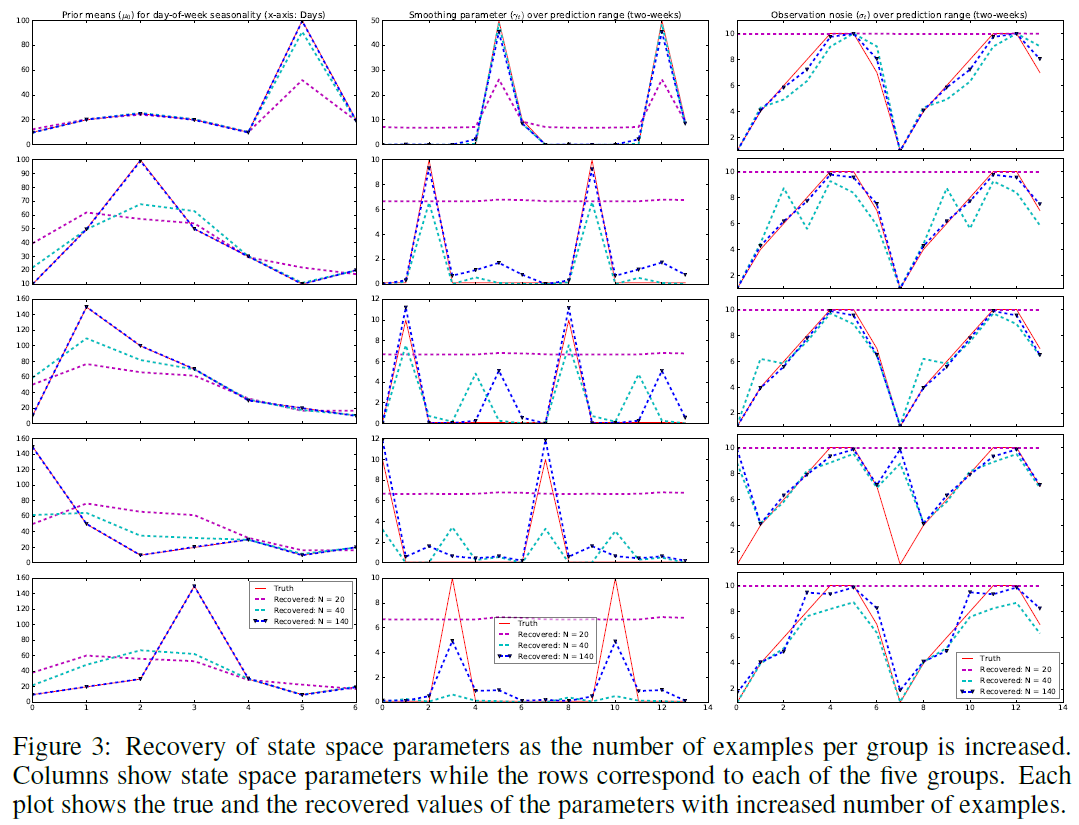
Quantitative experiments
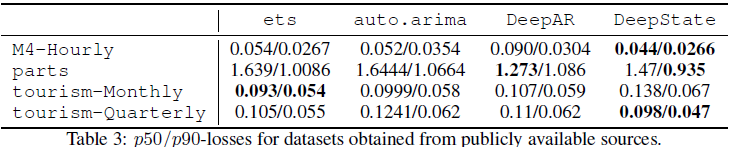
공개된 시계열 데이터 traffic과 electricity 에 대해 기존 baseline과의 정량적인 비교 실험을 수행합니다. 이때, latent space의 차원은 데이터의 주어진 계절성 주기에 따라 결정됩니다. (시간 단위면 24, 주 단위면 7 등) 훈련 범위를 14일, 21일, 28일로 조절하면서 다음 7일 동안의 예측치와 실제값의 $\rho-$ quantile loss를 통해 성능을 비교합니다.


다른 baseline 방법에 비해서 DeepState 방법의 성능이 제일 좋은 것을 알 수 있습니다. 특히 auto.arima 같은 전통적인 모형들은 여러 시계열의 공통된 패턴을 학습할 수가 없으므로 안 좋은 성능이 나오지 않았나 추정됩니다. 또한, DeepState는 여러 시계열의 공통된 패턴을 학습할 수 있으므로 하나의 도메인의 다양한 시계열 데이터에 대한 성능을 비교하였고 다른 baseline에 비해 좋은 성능을 보였습니다.
홍머스 정리
- 시계열 데이터를 보고 계절성, 추세 등에 따라 latent space 차원을 설정해 주어야 함
- Day of week: 7 seasons, Hour of day: 24 seasons
참조
'Machine Learning Tasks > Time Series' 카테고리의 다른 글
| 파이썬에서 SARIMA 실행하기 - SARIMAX (5) | 2021.03.31 |
|---|---|
| Augmented Dickey-Fuller Test - Stationary 확인 (0) | 2021.03.30 |
| Multivariate Time Series (1) - 기본 확률 (0) | 2021.03.13 |
| Exponential Smoothing, CMA, Winter's Method (0) | 2021.03.12 |
| Nonstationary process, ARIMA, SARIMA (0) | 2021.03.11 |


