BERT, GPT, ViT 모델에서는 인코더 블락 안의 2-layer MLP 구조의 활성화 함수로 ReLU가 아닌 GELU (Gaussian Error Linear Unit) 함수가 사용됩니다. 최신 NLP, Vision SOTA 성능을 도출하는 모델들이 GELU 함수를 사용하면서 최근에 발표된 것이 아닌가 싶지만 arxiv 상에서는 16년 6월에 올라온 나름 오래된 함수입니다. 입력 $x$의 부호에 대해서 self-gating 하는 ReLU 함수와 달리 ($x 1_{x>0}$) GELU 함수는 $x\Phi (x)$ 형태로 정의되는데요, 한번 살펴보도록 하겠습니다.
GELU 함수는 dropout, zoneout, ReLU 함수의 특성을 조합하여 유도되었습니다. 먼저 ReLU 함수는 입력 $x$의 부호에 따라 1이나 0을 deterministic 하게 곱하고 dropout 은 1이나 0을 stochastic 하게 곱합니다. 따라서 GELU 에서는 이 두 개념을 합쳐 $x$에 0또는 1로 이루어진 마스크를 stochastic 하게 곱하면서도 stochasticity 를 $x$의 부호가 아닌 값에 의해서 정하고자 합니다. 구체적으로 $x$에 $m \sim Bernoulli(\Phi (x))$ 을 곱합니다. $\Phi(x) = P (X\leq x), X \sim$ N(0,1) 는 표준정규분포의 CDF (Cumulative Distribution Function) 으로 배치 정규화 이후에 $x$가 일반적으로 정규분포 양상을 띄기 때문에 $X$의 분포로 선택했다고 합니다. 따라서 $x$가 줄어들수록 $\Phi(x)$가 줄어드므로 $x$가 dropped 될 확률이 높아지겠죠. 즉, 초기 의도대로 stochastic 특성을 유지하면서 그 특성이 입력값에 의존하도록 만들었습니다.
하지만 neural networks 활성화 함수로 사용되기 위해서는 deterministic 함수를 원합니다. Dropout 때와 같이 stochacity 에 확률에 따른 평균을 취하면 $\Phi (x) \times x + (1-\Phi (x)) \times 0=x\Phi (x)$가 됩니다. 또한, CDF $\Phi$ 함수는 error 함수로 Equation 1과 같이 정의되고, 이를 Equation 2와 같이 근사할 수 있습니다.

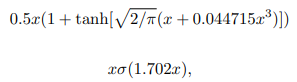
Equation 2로 근서한 GELU 함수 형태는 Figure 1과 같습니다. Mish / Swish 함수와 굉장히 비슷한데, 1) bounded below, 2) non-monotonic, 3) unbounded above, 4) smooth 특성을 모두 갖습니다.

GELU 논문을 보면 NLP, Vision 다양한 태스크에 대해 GELU 함수가 ReLU, ELU 에 비해 일관적으로 성능이 좋습니다. GELU 에서 CDF 함수를 정의할 때 사용한 $X\sim N(0,\sigma)$의 $\sigma\rightarrow 0$ 이라하면 ReLU 가 된다는 점을 보아 GELU 는 ReLU 의 smoothing 버젼이라 볼 수 있습니다. (표준정규분포의 $\sigma$가 작아질수록 CDF 모양이 ReLU 의 $1_{x>0}$과 모양이 매우 비슷해집니다.) 또한, ELU 같은 경우는 GELU 에서의 CDF 함수를 $Cauchy(0, 1)$에 대해서 정의하면 유도할 수 있습니다.
하지만 GELU 함수가 ReLU, ELU 와 확연히 구분되고 최근에 등장한 Mish / Swish 활성화 함수와 비슷한 특징은 1) 모든 점에서 미분 가능하고, 2) 단조증가함수가 아니라는 점이고 이는 비선형 활성화 함수 목적에 맞게 더욱 복잡한 전체 함수를 모델링하는데 더 도움이 됩니다. 또한, ReLU 함수는 $x$의 부호에 대해서 gating 되는 것과 달리 GELU 함수는 $x$가 다른 입력에 비해서 얼마나 큰지에 대한 비율로 gating 되니 확률적인 해석이 가능해지고 함수 형태가 미분가능하게 됩니다.
Sigmoid / tanh 활성화 함수가 bounded 되어있어 vanishing gradient 현상을 유발하고 이를 대체하기 위해 ReLU 활성화 함수가 폭넓게 사용되고 있지만 ReLU 는 입력이 음수가 되어버리는 순간 기울기가 0이므로 그 노드에 연결된 파라미터들이 업데이트가 되지 않습니다. 이러한 현상이 neural networks 에서 매우 폭넓게 발생해 neuron 대부분이 0이 되버리는 sparsity 가 발생할 때를 dying ReLU 현상이라고 합니다. 이 경우는 자주 일어나지는 않지만 1) 매우 큰 learning rate 를 가지거나, 2) 매우 큰 음수 bias 항을 가지는 경우에 ReLU 입력이 급격하게 음수가 되어버릴 때 주로 발생합니다.
따라서 이를 극복하기 위해 Leaky ReLU 같이 음수 부분에 작은 기울기를 주는 활성화 함수가 개발이 되었지만 이 함수들은 음수에 대해서 bounded (bounded below) 되어있지 않기에 feature 학습에 부정적인 영향을 끼칠 가능성이 있습니다. (음수가 곱해지는 것이 누적되면 최종적이 활성화가 잘 되지 않을 것이니까요.) 따라서 GELU, Mish, Swish 같이 음수 부분이 값을 가지지만 너무 커지지 않게 bounded 하면서 기울기가 잘 정의되어 있는 함수가 점점 넓게 사용되고 BERT, GPT 같은 SOTA 모델에 대해서 사용되었습니다. 하지만 어떤 활성화 함수가 만능이다, 무조건 써야한다라는 정답은 아직까지는 없는 것 같습니다.
참조
'Machine Learning Models > Techniques' 카테고리의 다른 글
| Open CLIP text embedding pooling (3) | 2024.03.04 |
|---|---|
| Smooth L1 Loss vs Huber Loss (0) | 2022.10.12 |
| Label Smoothing (0) | 2021.06.15 |
| CutMix (0) | 2021.06.10 |
| Mish (0) | 2021.06.06 |


