Smooth L1 Loss vs Huber Loss

일반적인 회귀 (regression) 훈련에는 예측값과 실제값 차이의 절댓값인 L1 loss나 예측값과 실제값 차이의 제곱인 L2 loss를 목적 함수로 사용하게 됩니다. 잘 알려져 있다시피 L2 loss는 모든 구간에서 안정적으로 미분이 가능하지만 제곱이 들어가는만큼 아웃라이어 (이상치)에 민감하게 반응하고, L1 loss는 아웃라이어에 L2 loss 대비 강건한 대신 미분이 불가능한 지점이 존재하고 평균 대신 중앙값 (median)을 추정하는 만큼 부정확한 요소가 존재합니다. 따라서 L1, L2 loss을 합친 Smooth L1 loss나 Huber loss가 제안되었습니다.

Huber Loss

Smooth L1 Loss

Huber loss, Smooth L1 loss 모두 L1과 L2의 장점 만을 합치고자 제안된 목적 함수로 공통적으로 예측값과 실제값 차이가 특정 임계치 (Huber 에서는 $\delta$, Smooth L1 에서는 $\beta$) 보다 작을 경우에는 L2 loss, 클 경우에는 L1 loss처럼 동작하게 됩니다. 다만, 형태가 살짝 다른게 Huber loss의 $\delta$는 L1 loss 부분에 붙어있지만 Smooth L1 loss의 $\beta$는 L2 loss 부분에 붙어있죠. 따라서 각 임계치 변화에 따라 Huber loss, Smooth L1 loss의 양상이 달라지게 됩니다.

Huber Loss

먼저 Huber loss에서 $\delta$ 값이 0.01, 0.1, 1, 10 으로 변화했을 때의 loss 변화 양상을 살펴보겠습니다. 

def huber(x_minus_y, delta=1):
    if np.abs(x_minus_y) < delta:
        return x_minus_y**2 / 2
    else:
        return delta*np.abs(x_minus_y) - delta**2 / 2

Huber loss는 L1 loss 부분에서 $\delta$가 곱해지기 때문에 기울기가 $\delta$가 됩니다. 따라서 $\delta$ 값이 커질수록 Huber loss는 L2 loss 처럼 동작하게 됩니다. 반면에 $\delta$ 값이 작아질수록 0에 거의 근접하게 됩니다. 

Smooth L1 Loss

마찬가지로 Smooth L1 loss의 $\beta$가 0.01, 0.1, 1, 10 으로 변화할 때의 양상을 살펴보겠습니다.

def smooth_l1(x_minus_y, beta=1):
    if np.abs(x_minus_y) < beta:
        return 0.5 * x_minus_y**2 / beta
    else:
        return np.abs(x_minus_y) - 0.5 * beta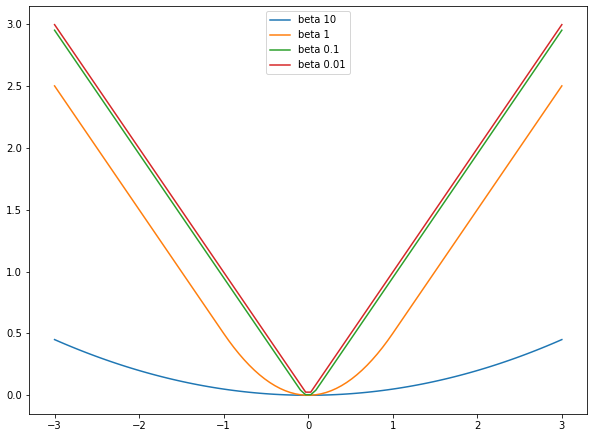

Smooth L1 loss에서는 $\beta$ 값이 커질수록 0에 근접하는 반면, $\beta$ 값이 작아질수록 L1 loss와 유사하게 동작합니다. 또한, 특이한 점으로는 $\beta$ 값에 상관없이 L1 loss 부분의 기울기가 1로 일정합니다. 이는 Huber loss와 다르게 $\beta$가 L2 loss 부분에 붙어있기 때문입니다. 극단적으로 $\beta=0$이 되면 Smooth L1 loss는 L1 loss와 같습니다. 따라서 Smooth L1 loss는 이름이 뜻하는 것처럼 기본적으로는 L1 loss 이고 예측값과 실제값 차이가 매우 작은 부분에 대해서만 L2 처럼 부드럽게 치환된 것이라 볼 수 있습니다.

 

참조

• https://pytorch.org/docs/stable/generated/torch.nn.SmoothL1Loss.html
• https://pytorch.org/docs/stable/generated/torch.nn.HuberLoss.html#torch.nn.HuberLoss
• https://stats.stackexchange.com/questions/539760/huber-loss-smooth-l1-properties