SimCLR, MoCo 포스트에서 살펴봤듯이 대조 학습 (contrastive learning)을 통한 비지도 representation 추출은 지도학습 성능에 거의 근접해가고 있습니다. 이러한 방법은 보통 학습이 진행되면서 타겟이 변하는 online (on-the-fly) 형태의 학습 방법을 취하고 positive/negative 샘플 간 비교를 위해 매우 큰 배치 사이즈가 필요하게 됩니다.
대조 학습을 위한 contrastive loss는 같은 이미지로부터 파생된 representation 쌍의 유사도를 높이고 다른 이미지로부터 파생된 쌍의 유사도를 낮추는 방향으로 진행됩니다. 원론적으로 이 방법을 큰 데이터셋에 대해 모두 적용하기에는 구현 상의 문제가 따르므로 큰 배치 사이즈를 설정하게 됩니다. SwAV 의 동기는 개별 이미지의 positive/negative 쌍을 직접적으로 비교하는 것이 아닌, 비슷한 feature를 가진 이미지를 군집화시켜 군집끼리 비교하자는 것입니다.
이번 포스트에서 다룰 SwAV (Swapping Assignments between multiple Views of the same image) 는 추출한 feature 들을 직접적으로 비교하지 않고 같은 이미지로부터 파생된 서로 다른 augmented 이미지에 cluster를 할당하여 서로의 cluster를 맞바꾸어 예측합니다. 또한 일반적으로 한 쌍의 transformation (augmentation) 을 적용하는 기존 방법과는 달리, multi-crop 이라는 새로운 augmentation 방법을 제안하여 ImageNet 에 대한 linear evaluation 결과가 지도학습에 거의 근접한 75.3%를 달성했습니다. (top-1 acuuracy)
Method
일반적인 군집화 (clustering) 과정은 군집화 훈련을 하는 과정과 모든 데이터에 대해 군집을 새로 할당하는 과정을 반복하는 offline 형태를 취합니다. 따라서 모든 데이터에 대해 feature 를 매번 새로 추출해야하는 과정을 거쳐야 하니 데이터가 들어오면서 매번 feature 변화를 업데이트 하는 online 학습에 부적합합니다. SwAV 는 이를 대체하여 같은 이미지에서 파생된 augmented 이미지 code의 (군집) 일관성을 강화하는 방향으로 학습을 진행합니다. 즉, code 자체를 타겟으로 삼지 않고 같은 이미지로부터 파생된 이미지들이 할당된 code 가 일관되도록 하자는 것이죠.
같은 이미지로부터 파생된 feature $z_t, z_s$와 이를 $K$ 프로토타입 ${c_1, ..., c_K}$를 통해 할당한 code $q_t, q_s$가 있을때, Equation 1과 같은 "swapped" 예측 문제를 제시합니다.
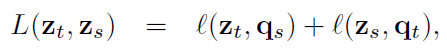
Equation 1을 보면 feature인 $z_t, z_s$를 직접적으로 비교하지 않고 code인 $q_t, q_s$를 통해 비교합니다. $z_t, z_s$가 비슷한 정보를 가지고 있다면 $q_t$를 $z_s$로 예측하는 것이 가능할 것이다라는 생각에서 유도된 것입니다.

Online clustering
각 이미지 $x_n$은 특정한 transformation $t$를 거쳐 ($x_{nt}$) encoder $f_\theta$를 통해 feature $z_{nt}$로 매핑됩니다. (이때 $z_{nt}$는 $f_\theta (x_{nt})$가 $L2$ 정규화된 값입니다) 그 이후에 $z_{nt}$과 훈련가능한 $K$개의 프로토타입 벡터 $C={c_1, ..., c_K}$를 통해 code $q_{nt}$를 계산합니다. SwAV의 핵심은 프로타타입 벡터와 code를 훈련과정 동안 online 방식으로 업데이트 하는 데 있습니다.
먼저 Equation 1의 $l(z_t, q_s)$를 어떻게 정의할 수 있을까요? $l(z_t, q_s)$는 feature $z_t$ 로부터 code $q_s$를 예측하는 것으로 $q_s$와 $z_t$, $C$로부터 얻은 softmax code 확률 간의 cross entropy loss로 정의할 수 있습니다. (Equation 2, $\tau$는 temperature 파라미터)
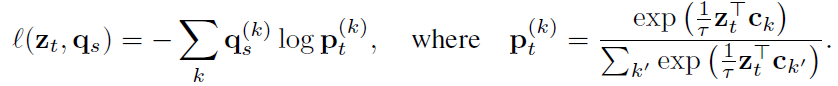
이를 Equation 1에 대해 배치안의 모든 데이터에 대해 적용하면 Equation 3과 같은 목적함수를 얻을 수 있고 $f_\theta$와 $C$에 대해 최소화됩니다.

Computing codes online
Online 학습이 가능하게 하기 위해서는 code를 배치 안의 샘플들로만 계산하여야 합니다. 따라서 $C$는 여러 배치들이 공유하게 되며 많은 샘플들이 $C$에 의해 code가 할당되게 됩니다. SwAV 는 모든 이미지가 같은 code로 매핑되는 trivial solution을 방지하기 위해 배치 안의 서로 다른 이미지들이 $C$에 의해 서로 다른 code로 균등하게 배분될 수 있게 합니다. 그렇다면 code를 어떻게 계산하여야 할까요?
배치 사이즈 $B$개의 feature 벡터 $Z=[z_1, ..., z_B]\in R^{D\times B}$와 $C$로 매핑된 code 벡터 $Q=[q_1,...,q_B]\in R^{K\times B}$가 있다고 할때, 먼저 $Z^{T} C$로부터 계산된 code와 $Q$의 유사도가 높아야 합니다. 이를 위해서 두 행렬 간의 내적 (inner product) $<Q,Z^{T} C>$가 최대화를 시킵니다. 또한, 배치 안의 샘플들이 서로 다룬 code로 균등하게 배분될 수 있도록 엔트로피 항 $H(Q)=-\sum_{ij} Q_{ij} log Q_{ij}$을 추가합니다. 크기가 같은 행렬 $A,B$에 대해 $<A,B>=Tr(A^{T} B)$ 인 것을 통해 Equation 4를 통해 code vector $Q$를 유도할 수 있습니다.

$\epsilon$을 너무 크게 한다면 엔트로피 항이 지나치게 정규화되어 모든 $Q_{ij}$가 같아버리는 trivial solution이 발생할 수 있기 때문에 $\epsilon$은 적당히 작게 유지합니다. 또한 $Q$에 대해 optimal transport를 이용할 수 있도록 다음과 같이 각 행/열의 합이 일정하도록 제약을 부여합니다.
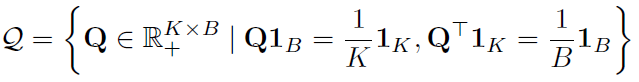
이러한 최적화 문제는 optimal transport 문제입니다. Optimal transport 문제는 서로 다른 분포를 가진 데이터셋이 있을 때 하나의 데이터셋을 다른 데이터셋으로 최적으로 옮기는 것으로 다음 그림에서 빨간색 데이터셋을 파란색 데이터셋으로 옮기기 위한 최적의 couping matrix $P$를 구하는 문제입니다.
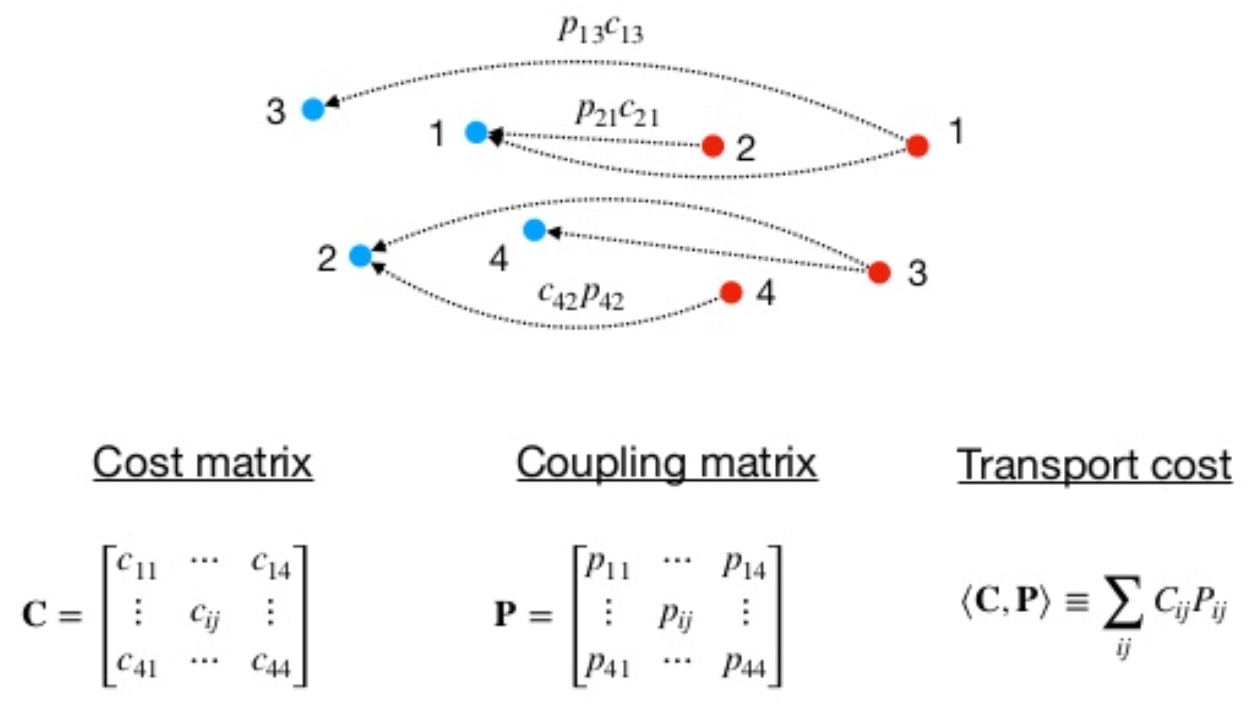
수식으로 표현하면 아래와 같이 수식화할 수 있고 이는 Sinkhorn-Knopp 알고리즘으로 풀 수 있습니다.


이를 SwAV에 적용하면 Equation 5와 같은 형태가 되고 Sinkhorn-Knopp 알고리즘을 통해 $Q^*$를 얻을 수 있으며, 3회의 반복만으로도 충분히 좋은 결과를 얻을 수 있었다고 합니다.
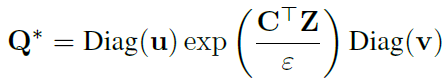

Multi-crop
일반적으로 한 이미지의 random crop을 비교하는 것은 이미지 전체의 정보를 포착하는데 중요한 역할을 하지만 다양한 random crop을 만들어 일일히 비교하기에는 계산 상의 부담이 매우 크게 됩니다. SwAV 에서는 multi-crop이라는 새로운 augmentation 기법을 제안합니다. Multicrop은 2개의 일반적인 random crop을 획득한 이후 $V$개의 해상도가 낮고 이미지의 매우 작은 부분만을 포함하는 추가적인 crop을 만들어냅니다.
$V+2$개의 crop에 대해서 모두 code를 계산하는 것이 아니라 일반적인 2개의 random crop에 대해서만 code를 계산하고 $V$개의 저해상도 crop은 Equation 6과 같이 code 예측을 위한 feature로만 사용합니다.

Algorithm
전체 구현은 다음과 같습니다.

홍머스 정리
- 할당된 code는 연속된 값으로 일반적인 offline 군집화에서는 rounding을 통해 discrete하게 만들지만 SwAV에서는 현재 배치에 대해 online 방식으로 학습하므로 따로 군집 결과인 code를 따로 discrete하게 만들지 않음.
- 배치 사이즈가 작으면 프로토타입 $K$에 대해 균등하게 나눌 수 없기 때문에 대략 지난 배치로부터 얻은 3000여개의 feature를 저장하고 있음. 당연히 목적함수에 반영되는 것은 현재 배치의 feature.
참조
- Unsupervised Learning of Visual Features by Constrasting Cluster Assignments
- www.slideshare.net/ssuser6a8016/20191019-sinkhorn
다음 포스트
[Machine Learning/Unsupervised Learning] - Self-Supervised Learning - SwAV (2)
'Machine Learning Tasks > Self-Supervised Learning' 카테고리의 다른 글
| Self-Supervised Learning - SwAV (2) (0) | 2021.04.20 |
|---|---|
| Self-Supervised Learning - MoCo v2 (0) | 2021.04.16 |
| Self-Supervised Learning - MoCo (2) (0) | 2021.04.16 |
| Self-Supervised Learning - MoCo (1) (0) | 2021.04.15 |
| Self-Supervised Learning - SimCLRv2 (2) (0) | 2021.04.09 |



